Хелпикс

Главная

Контакты

Случайная статья



Лекция № 14.. Вычисление интегралов от тригонометрических функций по периоду

Стр 1 из 2Следующая ⇒


Лекция № 14.

1.Вычисление интегралов от тригонометрических функций по периоду

Рассмотрим интеграл вида

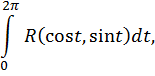
где 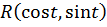– рациональная функция. Для вычисления таких интегралов в математическом анализе в общем случае, за исключением некоторых частных случаев, применяется замена  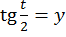(«универсальная» подстановка) и интеграл приводится к интегралу от рациональной дроби, а далее применяется соответствующий алгоритм интегрирования с простыми, но трудоемкими процедурами.

С другой стороны, отрезок 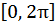 изменения переменных можно рассматривать как изменение  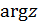точки 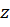, принадлежащей окружности. Действительно, замена  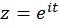переводит отрезок  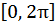в окружность  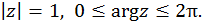При этом для переменных  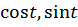получаются несложные, причем рациональные, выражения через 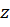. По формулам Эйлера получаем

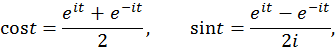
то есть

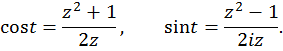
Из 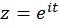 получаем 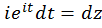, а поэтому 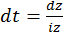. В результате получаем формулу, связывающую интеграл от действительной переменной с интегралом по замкнутой кривой от функции комплексного переменного

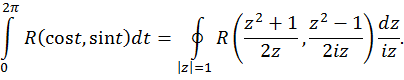
Полученный справа интеграл есть интеграл от рациональной функции, особыми точками которой являются только полюсы.

 

Пример 1. Вычислить интеграл

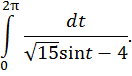
Решение. Сделаем замену переменных

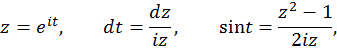
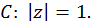
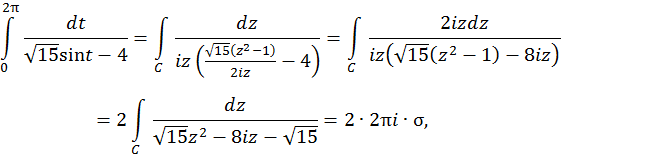
где 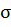 – сумма вычетов относительно полюсов подынтегральной функции, заключенных внутри окружности .

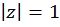Найдем полюса подынтегральной функции

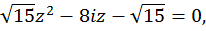
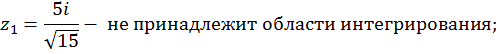
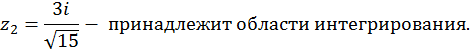
Таким образом, внутри окружности 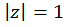 находится только один полюс кратности 1 – точка .

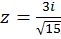Найдем вычет функции в этой точке

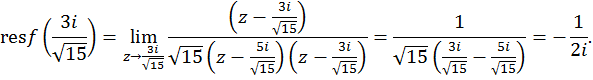
Тогда заданный интеграл равен

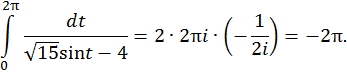
Пример 2. Вычислить интеграл

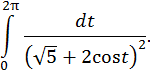
Решение. Сделаем замену переменных

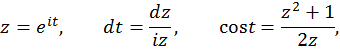
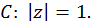
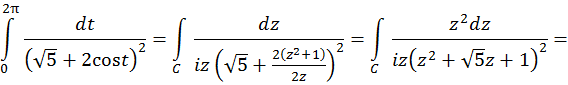
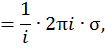
где 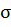– сумма вычетов относительно полюсов подынтегральной функции, заключенных внутри окружности .

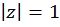Найдем полюса подынтегральной функции

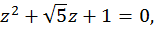
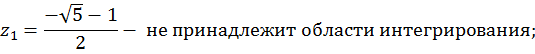
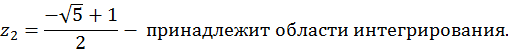
Таким образом, внутри окружности 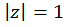 находится только один полюс второго порядка – точка .

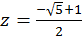Найдем вычет функции в этой точке

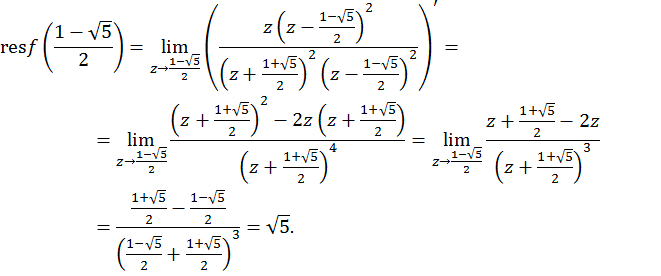
Тогда заданный интеграл равен

 


12Следующая ⇒
  

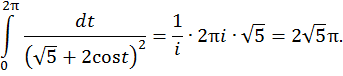
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.