
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Критерий Найквиста для статических и астатических систем
Критерий Найквиста для статических и астатических систем
Позволяет установить по АФХ разомкнутых систем необходимое и достаточное условие устойчивости замкнутых систем.
Его еще называют амплитудно-фазовым критерием устойчивости.
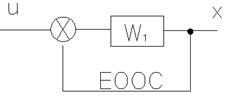
Имеем разомкнутую систему


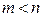
Замкнем систему:
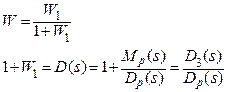
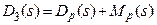 - характеристический полином для замкнутой системы
- характеристический полином для замкнутой системы
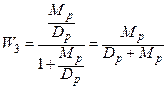 . Нас всегда интересуют полюсы (корни знаменателя).
. Нас всегда интересуют полюсы (корни знаменателя).
У них один порядок (n)
Обозначим корни характеристических уравнений для:
· Замкнутой системы àS’i
· Разомкнутой à Si
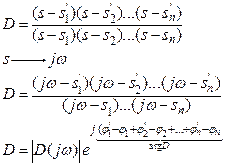
K – разом.
K’– замкн.

Найквист предложил:
Рассмотрим D(jω) в виде
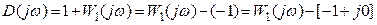
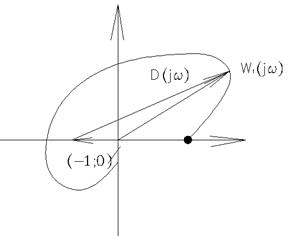
Рассмотрим 2 варианта:
1. Разомкнутая система устойчива. K=0 (все корни слева).
Чтобы замкнутая система была устойчива, необходимо, чтобы приращение аргумента вектора D=-πk’=0=>k’=0
Если разомкнутая система устойчива, то для устойчивости замкн. необходимо, чтобы АФК разомкнутой системы не охватывало критическую точку (-1;0)
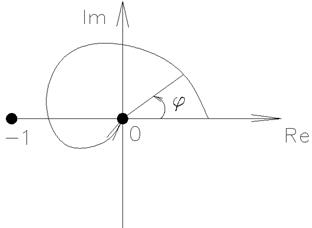
Приращение φ=0
2). Разомкнутая система неудобства. Тогда для устойчивости в замкнутом состояни и необходимо и достаточно, чтобы все корни замкнутой системы были слева => 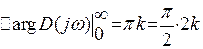
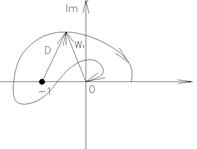
Неустойчивая разомкнутая система с k корнями в правой полуплоскости, будет устойчива в замкнутом состоянии, если АФК разомкнутой системы при возрастании ω от 0 до ∞. Охватит критическую точку против часовой стрелки 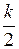 раз.
раз.
1) K=2
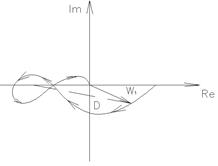
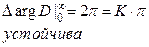
2) K=1
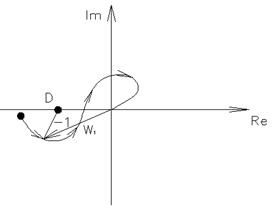
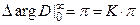
Устойчива (в замкнутом состоянии).
3) K=1

Приращение по часовой стрелке => -π
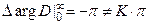
Неустойчива.
4) K=2
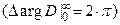
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|