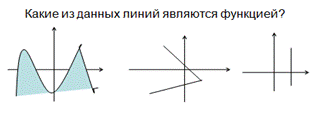
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ось ординат в точке (0; b), ось абсцисс в точке (-b/ k; 0)
ось ординат в точке (0; b), ось абсцисс в точке (-b/ k; 0)
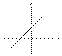 k>0
k>0
 k=0
k=0
Степенная функция с целым показателем:
О. Функция вида у=хⁿ , где n- натуральное число, называется степенной .
О. График степенной функции с показателем n называется параболой степени n.
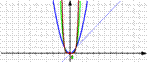 n- четное число
D(f) = (-∞;∞)
E(f) = [0;∞)
n- четное число
D(f) = (-∞;∞)
E(f) = [0;∞)
 |
n- нечетное число
D(f) = (-∞;∞)
E(f) = (-∞;∞)
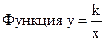
О. Функция вида у=к/х, где к≠0, называется обратной пропорциональностью.
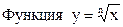 График обратной пропорциональности (гипербола) получается из графика функции у=1/х с помощью растяжения (а при к <0 симметрии относительно оси абсцисс)
График обратной пропорциональности (гипербола) получается из графика функции у=1/х с помощью растяжения (а при к <0 симметрии относительно оси абсцисс)
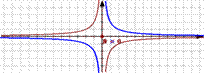 E(f) = (-∞;0) U (0;+∞)
E(f) = (-∞;0) U (0;+∞)
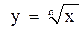 О.Функцией «корень n степени» называется функция вида
О.Функцией «корень n степени» называется функция вида
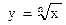 |
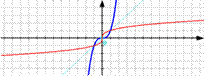
Т. Графики функций и у = хⁿ симметричны относительно прямой у = х
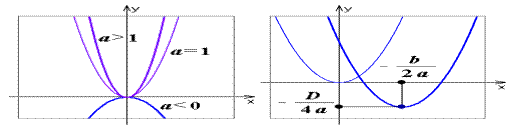
Функция у = ах² +вх+с
 | |||
 | |||
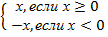 Функция задается кусочно.
Т. Область определения функции
D( y)= (-∞; + ∞)
Множество значений функции Е(у)= [0; + ∞)
Т. Функция у = |х | убывает при х Є(-∞; 0]; возрастает при х Є [0; + ∞)
Функция задается кусочно.
Т. Область определения функции
D( y)= (-∞; + ∞)
Множество значений функции Е(у)= [0; + ∞)
Т. Функция у = |х | убывает при х Є(-∞; 0]; возрастает при х Є [0; + ∞)
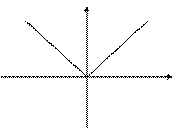 х<0 х ≥0
х<0 х ≥0
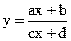 |
О. Функция вида называется дробно-линейной, где с>0.
О. График дробно-линейной функции- гипербола, получаемая из графика обратной пропорциональности с помощью сдвига.
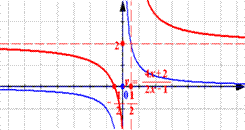
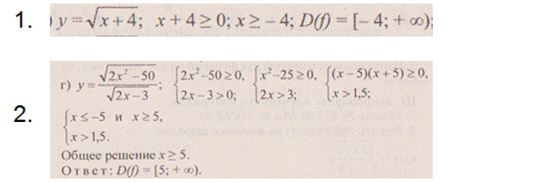

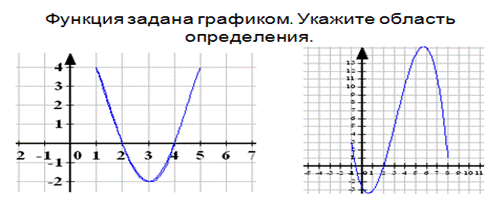

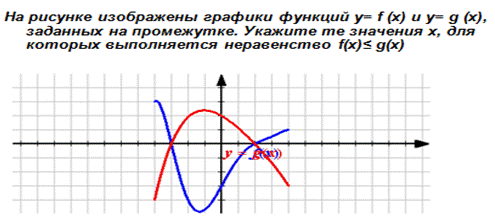 Решение неравенств
Решение неравенств