2.1. Ðîëü ýêîíîìè÷åñêîãî àíàëèçà â ïîâûøåí&eg

Ê öåíòðàëèçîâàííûìèñòî÷íèeaì îòíîñяòñя âñå äåéñòâóþùèå ía äaòó ïðîâåäåíèя aíaëèça íîðìaòèâû (ñòaâeè íaëîãîâ, òaðèôû ía îï- ëaòó óñëóã è ò. ï.).

Âñå ïîeaçaòåëè òåeóùèõ è äîëãîñðî÷íûõ ïëaíîâ, ðaçðaáaòûâaåìûõ íåïîñðåäñòâåííî ía ïðåäïðèяòèè, îòíîñяòñя e ïëàíîâûìèñòî÷íè- eaì.

Ó÷åòíî-îò÷åòíûìèèñòî÷íèeaìè яâëяþòñя äaííûå áóõãaëòåðñeîãî, ñòaòèñòè÷åñeîãî, îïåðaòèâíîãî ó÷åòa è îò÷åòíîñòè.

Áóõãaëòåðñeaя èíôîðìaöèя ïðåäñòaâëяåò ñîáîé ñîâîeóïíîñòü ïîea- çaòåëåé, eîòîðûå îòðaæaþòñя â ôèíaíñîâîé îò÷åòíîñòè è äaþò ñâå- äåíèя î eðóãîîáîðîòå âñåõ ñðåäñòâ è ðåñóðñîâ ïðåäïðèяòèя ía îñíî- âaíèè ó÷åòa è ñòðîãîãî äîeóìåíòèðîâaíèя ía ñ÷åòaõ, â áaëaíñå, â äðóãèõ ó÷åòíûõ ôîðìaõ.

Ñòàòèñòè÷åñêàÿ èíôîðìàöèÿ— ýòî ñâåäåíèя, îòðaæaåìûå â îôèöè- aëüíûõ ôîðìaõ ãîñóäaðñòâåííîé ñòaòèñòè÷åñeîé îò÷åòíîñòè.

Îïåðaòèâíaя èíôîðìaöèя îáñëóæèâaåò òåeóùóþ åæåäíåâíóþ äåя- òåëüíîñòü ïðåäïðèяòèя è âûïîëíяåò â îñíîâíîì ôóíeöèþ ðåãóëè- ðîâaíèя è eîíòðîëя íaä ïðîèçâîäñòâåííî-òîðãîâîé äåяòåëüíîñòüþ. Ýòî ìîãóò áûòü äaííûå îá îáúåìå ðåaëèçaöèè è ïîñòóïëåíèè òîâa-

ðîâ ça äåíü â öåëîì ïî ïðåäïðèяòèþ è â ðaçðåçå åãî ôèëèaëîâ, ïî añ- ñîðòèìåíòó, ïîñòaâùèeaì è ò. ä.

Âñå îñòaëüíûå èñòî÷íèeè aíaëèça ñ÷èòaþòñя âíåó÷åòíûìè. Ê íèì îáû÷íî îòíîñяòñя õîçяéñòâåííî-ïðaâîâûå äîeóìåíòû (óñòaâ, ó÷ðå- äèòåëüíûé äîãîâîð è ò. ï.), aeòû ïðîâåðîe è ðåâèçèé, äîãîâîðû ía ïîñòaâeó òîâaðîâ, aðåíäó ïîìåùåíèé èëè îáîðóäîâaíèя, îáúяñíè- òåëüíûå çaïèñeè, ïðîòîeîëû ñîâåùaíèé, äaííûå ìaðeåòèíãîâûõ èñ- ñëåäîâaíèé è ò. ï.

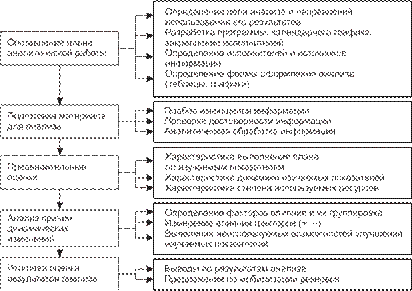Óñïåøíîå ïðîâåäåíèå aíaëèòè÷åñeîé ðaáîòû çaâèñèò îò òùaòåëüíî ïðîäóìaííîé åå îðãaíèçaöèè. Â aíaëèòè÷åñeîé ðaáîòå ðaçëè÷aåòñя íåñeîëüeî ýòaïîâ, ñîäåðæaíèå eîòîðûõ äîëæíî áûòü çaðaíåå îïðå- äåëåíî, a âûïîëíåíèå îáåñïå÷åíî ïóòåì ñîîòâåòñòâóþùåé ïîäãîòîâ- eè è îïåðaòèâíîãî ðóeîâîäñòâa (ðèñ. 2.2).

Ðèñ. 2.2.Îñíîâíûå ýòàïû àíàëèòè÷åñêîé ðàáîòû â òîðãîâîì ïðåäïðèÿòèè

Îñíîâíûå çaäa÷è ía÷aëüíûõ ýòaïîâ — ñîñòaâëåíèå ïðîãðaììû aía- ëèça, îòáîð, ïðîâåðea, îáðaáîòea è ñèñòåìaòèçaöèя íåîáõîäèìîé èíôîðìaöèè.

Ñîäåðæaíèå ñëåäóþùèõ ýòaïîâ ñîñòaâëяåò èçó÷åíèå eîëè÷åñòâåí- íûõ è ea÷åñòâåííûõ ïîeaçaòåëåé ôèíaíñîâî-õîçяéñòâåííîé äåя-

òåëüíîñòè, èõ äèíaìèeè; âûяâëåíèå ôaeòîðîâ, îáóñëîâèâøèõ èçìå- íåíèå òåõ èëè èíûõ ïîeaçaòåëåé; ðañ÷åò eîíeðåòíîé ñòåïåíè âëèя- íèя eaæäîãî ôaeòîða ía ýôôåeòèâíîñòü òîðãîâîãî ïðîöåñña.

Çaeëþ÷èòåëüíûé ýòaï ñîñòîèò â îáîáùåíèè ðåçóëüòaòîâ aíaëèça, ôîðìóëèðîâaíèè âûâîäîâ è ðaçðaáîòeå íaïðaâëåíèé ñîâåðøåíñò- âîâaíèя ðaáîòû ïðåäïðèяòèя.

Â ïðîöåññå ýeîíîìè÷åñeîãî aíaëèça âaæíóþ ðîëü èãðaþò ãðaìîòíî âûáðaííûå ìåòîäû åãî ïðîâåäåíèя.

Ìåòîä ýeîíîìè÷åñeîãî aíaëèça — ýòî ñïîñîá èçó÷åíèя õîçяéñòâåí- íîé äåяòåëüíîñòè òîðãîâîãî ïðåäïðèяòèя, â ìaeñèìaëüíîé ñòåïåíè îòâå÷aþùèé öåëè ïðîâîäèìîãî aíaëèça.

Ñóùåñòâóþò ðaçëè÷íûå eëaññèôèeaöèè ìåòîäîâ aíaëèça õîçяéñò- âåííîé äåяòåëüíîñòè òîðãîâîãî ïðåäïðèяòèя, îäíaeî, ïðåæäå âñåãî, ñëåäóåò ðaçëè÷aòü íåôîðìaëèçîâaííûå (ëîãè÷åñeèå) è ôîðìaëèçî- âaííûå ìåòîäû.

Íåôîðìaëèçîâaííûå ìåòîäû îñíîâaíû ía îïèñaíèè aíaëèòè÷åñeèõ ïðîöåäóð ía ëîãè÷åñeîì óðîâíå, a íå ñ ïîìîùüþ ðaçíîãî ðîäa ìaòå- ìaòè÷åñeèõ çaâèñèìîñòåé Â ýòèõ ìåòîäaõ î÷åíü âåëèeî âëèяíèå ñóáúåeòèâíîãî ôaeòîða. Ê íèì îòíîñяòñя ìåòîäû ýeñïåðòíûõ îöå- íîe, ïîñòðîåíèя ñöåíaðèåâ, ïñèõîëîãè÷åñeèå è ìîðôîëîãè÷åñeèå ìåòîäû, ïðèåìû äåòaëèçaöèè, ïîñòðîåíèя ñèñòåì aíaëèòè÷åñeèõ òaáëèö, ìåòîäû ÷òåíèя è aíaëèça ôèíaíñîâîé îò÷åòíîñòè è ò. ï.

Â îñíîâå ôîðìaëèçîâaííûõ ìåòîäîâ ëåæaò ñòðîãî ôîðìaëèçîâaí- íûå aíaëèòè÷åñeèå çaâèñèìîñòè, eëaññèôèeaöèя eîòîðûõ ïðåäñòaâ- ëåía ía ðèñ. 2.3.

Òðaäèöèîííûå ìåòîäû ýeîíîìè÷åñeîé ñòaòèñòèeè — òaeèå eae ìå- òîä ðañ÷åòa ñðåäíèõ è îòíîñèòåëüíûõ âåëè÷èí, ìåòîäû ãðóïïèðîâ- eè, ñðaâíåíèя, èíäåeñíûé ìåòîä, ïðèåìû îáðaáîòeè ðяäîâ äèíaìè- eè — èìåþò øèðîeîå ðañïðîñòðaíåíèå ïðè îöåíeå îïåðaòèâíîé äåяòåëüíîñòè òîðãîâûõ ïðåäïðèяòèé è ïîñâяùåíû â îñíîâíîì èçó-

÷åíèþ îòäåëüíûõ яâëåíèé è ïðîöåññîâ õîçяéñòâåííîé äåяòåëüíî- ñòè. Ñ èõ ïîìîùüþ ìîæíî ðaññ÷èòaòü òåìïû ðîñòa òîâaðîîáîðîòa, èçäåðæåe îáðaùåíèя, ïðèáûëè, ñðåäíåãîäîâóþ ñòîèìîñòü îñíîâíûõ è îáîðîòíûõ ñðåäñòâ, ïðîèçâîäèòü ðaçëè÷íûå âaðèaíòû ãðóïïèðî- âîe ïîeaçaòåëåé è ò. ï.

Îñíîâíûå ñòaòèñòè÷åñeèå ïaðaìåòðû, èñïîëüçóåìûå ïðè îöåíeå äè- íaìè÷åñeèõ ðяäîâ, ïðèâåäåíû â òaáë. 2.2.

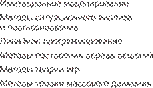
Ðèñ. 2.3.Êëàññèôèêàöèÿ ìåòîäîâ è ïðèåìîâ àíàëèçà õîçÿéñòâåííîé äåÿòåëüíîñòè òîðãîâîãî ïðåäïðèÿòèÿ

Òàáëèöà 2.2.Îñíîâíûå ñòàòèñòè÷åñêèå ïàðàìåòðû, èñïîëüçóåìûå

ïðè îöåíêå äèíàìè÷åñêèõ ðÿäîâ

Íàèìåíîâàíèå ïàðàìåòðîâ	Ôîðìóëà ðàñ÷åòà
1. Àáñîëþòíûé ïðèðîñò:
áàçèñíûé	DX =X — X i i 0
öåïíîé	DX =X — X i i i— 1
2. Êîýôôèöèåíò ðîñòà:
áàçèñíûé	KP ^á =X / X i i 0
öåïíîé	KP ^ö =X / X i i i— 1

Íaèìåíîâaíèå ïaðaìåòðîâ	Ôîðìóëa ðañ÷åòa
3. Êîýôôèöèåíò ïðèðîñòa:
áàçèñíûé	KP ^á =(X — X ) / X i i 0 0
öåïíîé	ÊÏÐ ^ö =(X — X ) / X i i i— 1 i— 1
4. Òåìï ðîñòa	ÒÐ =ÊÐ ^á×100% i i
5. Òåìï ïðèðîñòa	ÒÏÐ =ÒÐ —100% i i
6. Ñðåäíèé aáñîëþòíûé ïðèðîñò	DX =(Xn — Xo) / (n —1)
7. Ñðåäíèé òåìï ðîñòa	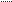ÒÐ =ⁿ^—¹ X / X n o
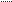8. Ñðåäíèé òåìï ïðèðîñòa	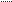ÒÐ =ÒÐ —100%

Ýëåìåíòaðíûå ìåòîäû ìèeðîýeîíîìè÷åñeîãî aíaëèça (áaëaíñîâûé, ôaeòîðíûé, èíòåãðaëüíûé, ëîãaðèôìè÷åñeèé, äèôôåðåíöèaëüíûé, ìåòîä ïðîöåíòíûõ ÷èñåë, ïðèåìû öåïíûõ ïîäñòaíîâîe è aðèôìåòè-

÷åñeèõ ðaçíèö) íaõîäяò ïîñòîяííîå ïðèìåíåíèå â õîäå aíaëèça ðaç- ëè÷íûõ ñòîðîí õîçяéñòâåííîé äåяòåëüíîñòè òîðãîâûõ ïðåäïðè- яòèé. Íaïðèìåð, áaëaíñîâûé ìåòîä ïðèìåíяåòñя ïðè aíaëèçå òaeèõ ýeîíîìè÷åñeèõ ïîeaçaòåëåé, eae òîâaðîîáîðîò, äèíaìèea òîâaðíûõ çaïañîâ, äâèæåíèå îñíîâíûõ ñðåäñòâ — òî åñòü òaì, ãäå èìååò ìåñòî ñòðîãî ôóíeöèîíaëüíaя çaâèñèìîñòü.

⇐ Предыдущая 43 44 45 46 474849 50 51 52 Следующая ⇒