Катер прошёл 108 км по течению реки и 84 км против течения. Скорость течения реки 3 км/ч . Найдите собственную скорость катера, если на путь по течению он затратил то же время, что и на путь против течения реки.. скорость. ФИЗКУЛЬТМИНУТКА (видео)

Тема урока: Решение задач с помощью дробных рациональных уравнений.

Цели и задачи урока:

Образовательные:

· закрепление понятия дробного рационального уравнения;

· продолжить формирование умений решать дробные рациональные уравнения;

· совершенствовать навык составления уравнения по условию задачи, уметь проверять соответствие найденного решения условиям задачи;

· сформировать умение решать задачи прикладного характера с помощью дробных рациональных уравнений.

Развивающие:

· развитие памяти обучающихся;

· развитие умений преодолевать трудности при решении математических задач;

· развитие любознательности;

· развитие логического мышления, внимания, умений анализировать, сравнивать и делать выводы;

· развивать интерес к предмету.

Воспитательные:

· формирование таких качеств личности, как ответственность, организованность, дисциплинированность, порядочность, правдивость;

· содействовать формированию системы знаний, представлений, понятий;

· воспитание познавательного интереса к предмету;

· воспитание самостоятельности при решении учебных задач;

· воспитание воли и упорства для достижения конечных результатов.

Тип урока: изучение нового материала.

Форма проведения:урок-практикум.

Форма организации учебно-познавательной деятельности:коллективная.

Оборудование урока: тестовые задания, презентация.

План урока:

1. Организационный момент;

2. Актуализация опорных знаний;

3. Этап изучения нового материала;

4. Физкультминутка;

5. Решение задач на закрепление пройденной темы;

6.Подведение итогов, рефлексия, Д/З.

Ход урока:

1. (Подготовка обучающихся к восприятию учебного материала) Приветствие, ориентация класса на работу, изложение плана работы на уроке.

Здравствуйте, ребята. Ещё начиная с начальной школы, вы учились решать задачи. Для этого с каждым годом вы обучались всё новым и новым методам и способам решения. Сегодня мы познакомимся с задачами, решение которых сводится к дробным рациональным уравнениям.

2. Эпиграфом нашего урока я взяла слова Генри Форда « Залогом успехаявляется, в первую очередь, хорошая подготовка»; они имеют отношение не только к предпринимательской деятельности, но и к учебной, в том числе и к изучению математики. Для того чтобы успешно решать задачи с помощью дробных рациональных уравнений, необходимо хорошо знать теорию решения этих самых уравнений. Поэтому повторим необходимые в дальнейшем понятия и формулы.

-Какие уравнения называются дробными рациональными?

-Алгоритм решения дробных рациональных уравнений:

1. Найти общий знаменатель дробей, входящих в уравнение.

2. Умножить обе части уравнения на общий знаменатель.

3.Решить получившееся уравнение.

4. Исключить проверкой из корней уравнения те, которые обращают в нуль общий знаменатель.

(Проведение самостоятельной тестовой работы)

1.Среди данных уравнений выберите то, которое не является дробным рациональным:

1) ;

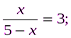
3) .

2.При каких значениях переменной х уравнение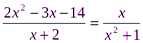

не имеет смысла: 1) -2; 2) -2 и -1; 3) всегда имеет смысл. (-2)

3.Сколько корней имеет уравнение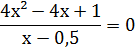

1) 1 корень; 2) не имеет корней; 3) 2 корня. (не имеет корней)

4. Найти корни уравнения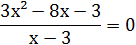

1) х=-⅓; 2) х=⅓ или х=-3; 3) х=-⅓ или х=3. (x=-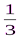

)

5.Укажите общий знаменатель:

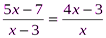1) х-3; 2) х(х-3); 3) (5х-7)(4х-3). (х(х-3))

Давайте сверим ответы с ответами на доске. На листочках ставим «+» или «-», в зависимости от правильности выполнения. Поставьте себе оценки:

все сделано правильно – «5»;

одна ошибка – «4»;

сделано две ошибки — «3»;

выполнено менее 3-х заданий – «2».

Давайте сделаем вывод: итак, вы научились решать дробные рациональные уравнения.Решать эти уравнения вы научились не зря, а для решения большого аппарата задач.

3. Запишите тему нашего урока «Решение задач с помощью дробных рациональных уравнений». Перед нами стоит задача: совершенствовать навык составления уравнения по условию задачи и умение проверять соответствие найденного решения условиям задачи.

Рассмотрим применение дробных рациональных уравнений при решении следующей задачи (задача записана на карточках, лежащих на столах у учеников):

Катер прошёл 108 км по течению реки и 84 км против течения. Скорость течения реки 3 км/ч . Найдите собственную скорость катера, если на путь по течению он затратил то же время, что и на путь против течения реки.

Для начала, давайте вспомним основные этапы решения задачи на составление уравнения. Нам известны три этапа. Какие это этапы?

Ученик: 1. Анализ условия, составление математической модели.

2. Работа с моделью.

3. Запись ответа.

Возвращаемся к нашей задаче.

Будем решать с помощью уравнения.

Обратите внимание на следующую таблицу (таблица выводится на экран. Слайд №5).

Обучающиеся постепенно заполняют таблицу, пользуясь знаниями из курса математики.

скорость

путь	время
V= S/ t	S= V t	t= S/ V

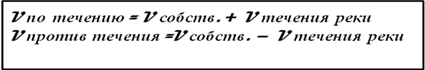Теперь давайте дадим полное пояснение нашим действиям (записывают в тетрадь):

Пусть x км/ч – собственная скорость катера.

Тогда (x+3)км/ч – скорость катера по течению, (x-3)км/ч – скорость катера против течения, 108/(х+3) ч — время движения катера по течению, 84/(х-3)ч — время движения против течения. Зная, что время движения по течению равно времени движения против течения, составим и решим уравнение: (слайд №6)

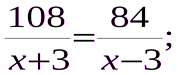
Решение:

108(х-3) = 84(х+3)

108х — 324 = 84х + 252

108х — 84х = 252+324

24х = 576

х = 24

ОДЗ: (х+3)(х-3) ≠ 0

х ≠ -3 и х ≠3

х = 24 (км/ч) – собственная скорость катера

Ответ: 24 км/ч.

4.ФИЗКУЛЬТМИНУТКА (видео)

Исходное положение-стойка ноги врозь. На счёт «раз» — руки отводятся назад. На счёт «два» — руки развести в стороны, на счёт «три» — поднять руки вверх, стать на носки. На счёт «четыре» — расслабляя плечевой пояс, руки опустить с небольшим наклоном вперёд. Повторить 4-6 раз в медленном темпе.

12 3 4 Следующая ⇒