Хелпикс

Главная

Контакты

Случайная статья



Доказать: .. Доказательство. Что и требовалось доказать.. Доказательство. Что и требовалось доказать.. Доказать: .. Доказательство. Что и требовалось доказать.

⇐ ПредыдущаяСтр 2 из 2


Доказать: .

Доказательство

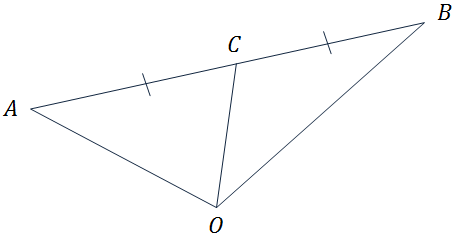
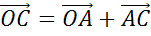
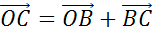
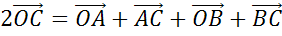
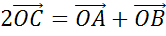
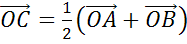
Что и требовалось доказать.

В следующей задаче докажем теорему о средней линии треугольника.

Задача. Доказать, что средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Доказательство

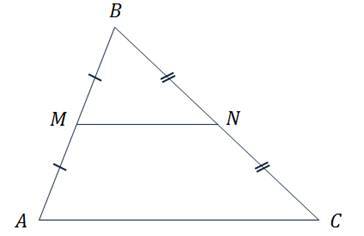
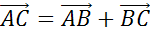
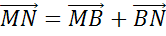
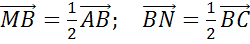
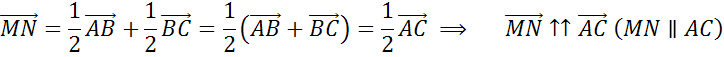
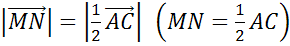
Что и требовалось доказать.

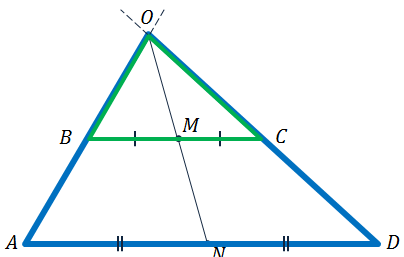
Задача. Доказать, что прямая, проведённая через середины оснований трапеции,

проходит через точку пересечения продолжений боковых сторон.

Доказать: .

Доказательство

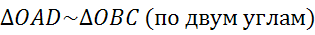
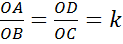
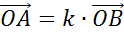
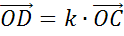
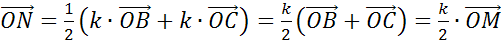
и 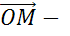коллинеарны

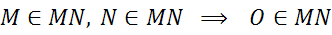
Что и требовалось доказать.

 

 

П р и м е ч а н и е . Результат задачи 2 можно использовать при доказательстве теоремы

о средней линии трапеции на следующем уроке.

 

 

Р е ш ен и е  

По условию AC : CB = 2 : 3, поэтому    

Но    

Следовательно,   откуда получается

 

П р и м е ч а н и е . Задача 3 является частным случаем более общей задачи 806.

 

Далее   

5. При наличии времени р е ш и т ь   задачу 4.

Точки    K, L, M, N – середины  сторон

 

 

Аналогично,  .

Из этих равенств следует, что   

Отсюда следует, что PQ || AE и PQ = AE.

 

 

 

 

 


⇐ Предыдущая12
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.