г. Тема: «Функции y = tgx, её свойства и график.”

11.11.2021г. Тема: «Функции y = tgx, её свойства и график.”

Цели: 1. Изучит свойства функций y = tgx, y = ctgx; выработать у учащихся умения изображать схематически и читать графики этих функций. Сформировать прочные навыки в умении решать графически уравнения, выполнять преобразования графиков.

Личностные результаты: сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;

Метапредметные результаты:умение самостоятельно определять цели своей деятельности, ставить и формулировать для себя новые задачи в обучении;

Предметные результаты: осознание значения математики для повседневной жизни человека;

Тип урока: урок открытия новых знаний.

Ход урока

1.Оргмомент.Сообщение темы, целей и задач урока. Приглашение к сотрудничеству.

2.Актулизация знаний. Устная работа.

1.Вычислите: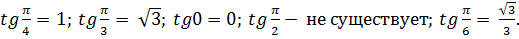

2.Докажите, что число p является периодом для функции .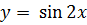

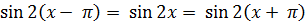
3.Докажите, что функция 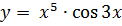нечётная. Доказательство: .

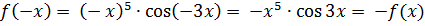4.Прочитайте свойства функции пографику.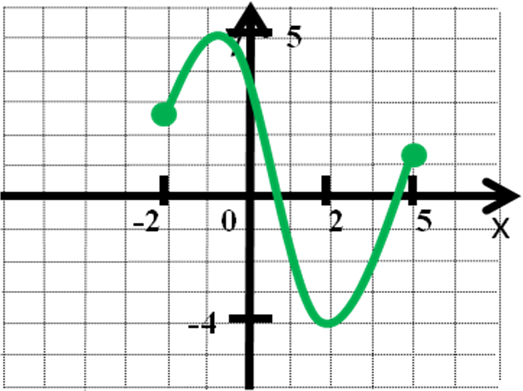

D(f) = [ -2; 5]. E(f) = [ -4; 5].Функция не является ни чётной, ни нечётной. Функция возрастает на промежутках [ -2; -1], [2; 5], убывает на промежутке [ -1; 2]. Функция ограничена снизу и сверху. 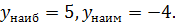Функция непрерывна на всей области определения.

3.Изучение нового материала. Начинаем со свойств функции y = tgx. Свойство 1. Какова область определения функции y = tgx? (Все действительные числа, кроме чисел вида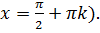

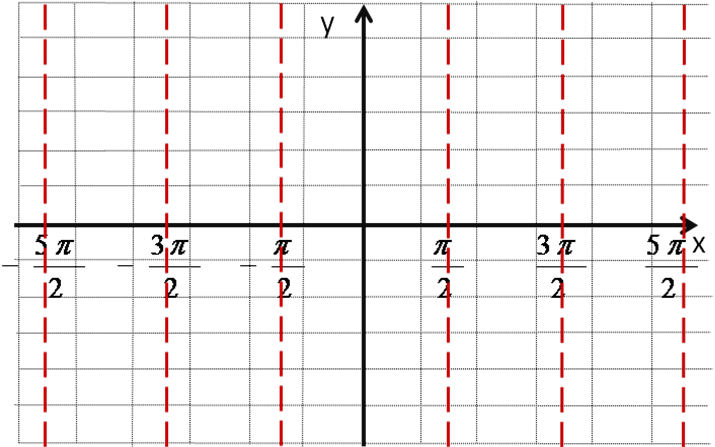
Свойство 2. Функция периодическая с периодом p, т.к.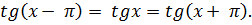

Свойство 3. Функция нечётная, т.к. 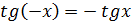. График нечётной функции симметричен относительно начала координат.

Составим таблицу основных значений:

x p/6 p/4 p/3

tgx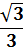

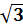
Построим график функции в первой четверти:

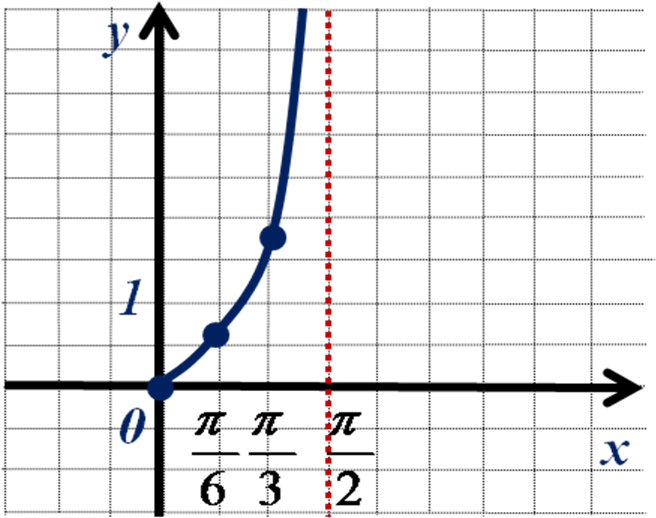
Используя свойства функции, строим полностью график функции y = tgx.

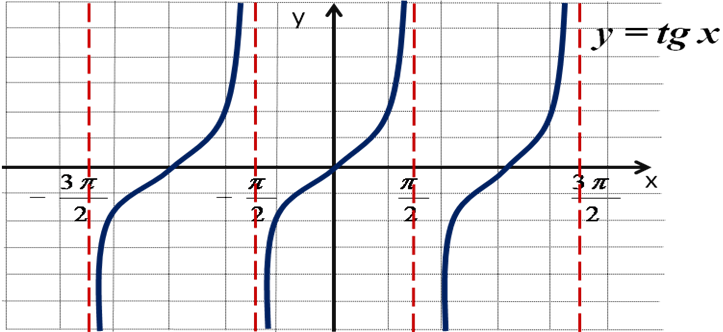
Свойство 4. Функция возрастает на всём интервале вида:

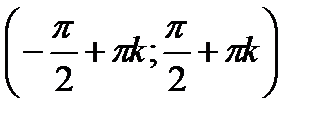
График функции y = tgx называют тангенсоидой, а ветвь на промежутке называют главной ветвью.

Свойство 5. Функция не ограничена ни снизу, ни сверху.

Свойство 6. Функция не имеет ни наибольшего, ни наименьшего значений.

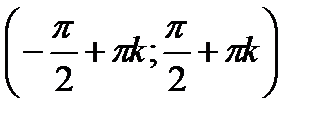Свойство 7.Функция y = tgx непрерывна на любом промежутке вида

Свойство 8. E(f) = ( - ¥; + ¥).

12 Следующая ⇒