
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лекция 10. D-разбиение в случае нелинейной зависимости коэффициентов от параметров.. Структурная устойчивость
Лекция 10
Пример 1: применяя метод разбиения оценить устойчивость в области А и В.
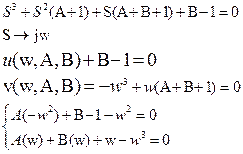
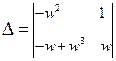

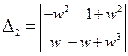
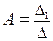
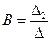
Особая прямая 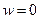
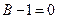
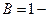 прямая // оси абсцисс
прямая // оси абсцисс
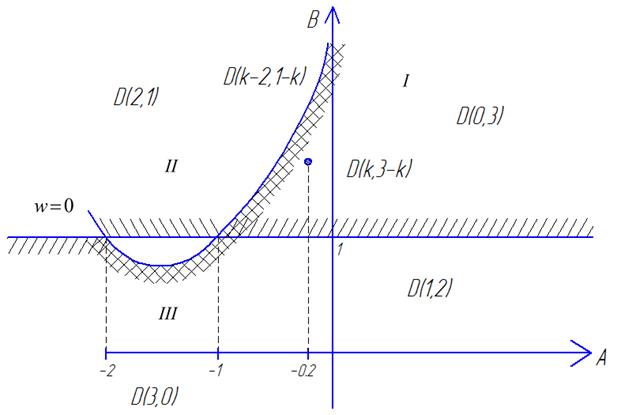
Исследуем (.) A=-0.2 B=2
По Гурвицу
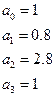
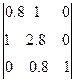
Пример 2:
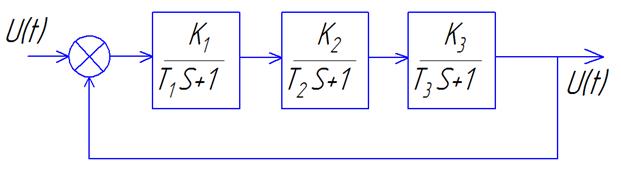

Оценить устойчивость замкнутой системы
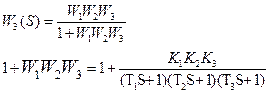
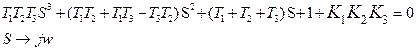
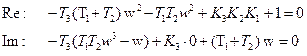
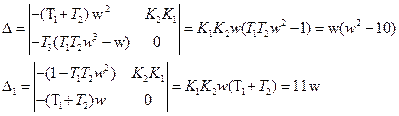
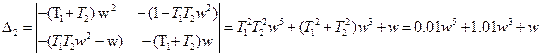
Особые прямые:
1) 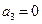 (w=0)
(w=0) 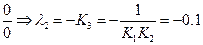
2) 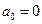 (w=0)
(w=0) 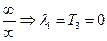
Из корней главного определителя следует, что
а) 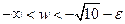
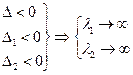
б) 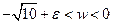
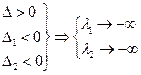
в) 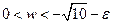
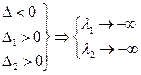
г) 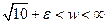
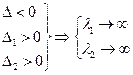
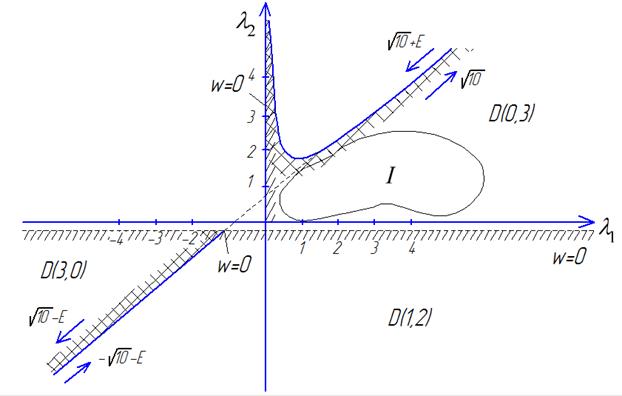
при w=0 меняет знак
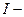 область претендент
область претендент
Исследовать точку (1,1) по Гурвицу
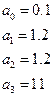
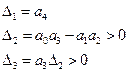
Из физических соображений, нас скорее всего заинтересует 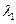 и
и 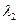
D-разбиение в случае нелинейной зависимости коэффициентов от параметров.
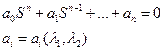
Коэффициенты должны существовать, быть конечными, непрерывно зависеть от 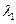 и
и 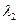 и однозначно ими определены (нет разрывов).
и однозначно ими определены (нет разрывов).
Способ построения D-кривой остается тем же, но, для определения границ допустимых значений, необходимо решить 2 нелинейных уравнения.
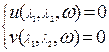 - в общем случае нелинейны.
- в общем случае нелинейны.
Эта система должна быть независима, должна существовать производная хотя бы 1 порядка и они должны быть непрерывны.
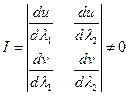

Пример: 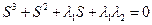

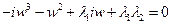
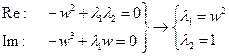
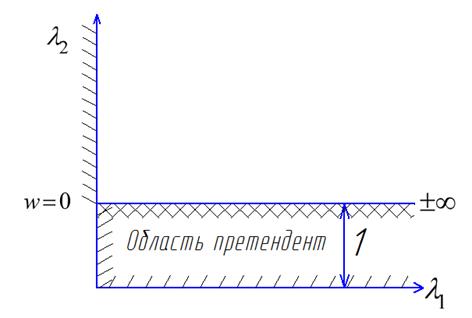
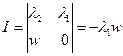
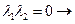 2 особые прямые
2 особые прямые 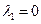
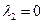
Если коэффициенты характеристического уравнения зависят от 3х и более параметров, то необходимо некоторые параметры замораживать, а остальные – менять, т.е. получать срезы гиперповерхностями àнаоборот D-областей.
Структурная устойчивость
Система, регулирование которой можно сделать устойчивыми, путем изменения их параметров, не изменяя ее структуры, называются структурно-устойчивыми. И наоборот, системы, которые невозможно сделать устойчивыми путем варьирования параметров, называют структурно-неустойчивыми.
Есть ряд правил, по которым можно сразу выявить структурную неустойчивость системы.
Например,
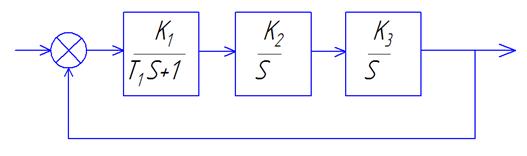
Подряд два интеграла.
Характеристическое уравнение
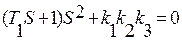
Если нет S в первой степени – не можем добиться устойчивости (математически доказано).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|