
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Скалярное поле. Производная по направлению. Градиент.
Скалярное поле. Производная по направлению. Градиент.
Векторное поле.
1. Производная в данном направлении.
Определение: Если функция U(x,y,z) дифференцируема, то производная от неё в направлении вектора 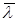 есть:
есть:
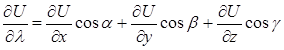 , где
, где 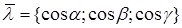
Задача. Найти производную скалярного поля 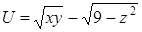 в точке
в точке 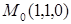 в направлении вектора
в направлении вектора 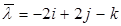
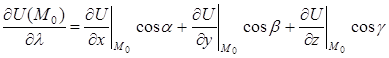
1. 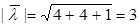 Þ
Þ 
2. 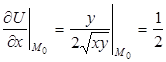 ,
,  ,
, 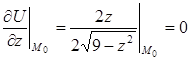
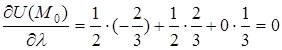
Задача. Найти производную скалярного поля 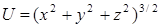 в точке
в точке 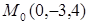 по направлению проходящей через эту точку нормали к поверхности
по направлению проходящей через эту точку нормали к поверхности 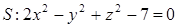 , образующей острый угол с положительным направлением оси Oz.
, образующей острый угол с положительным направлением оси Oz.
1. Т.к. нормаль задана как внешняя, то
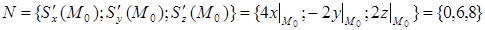
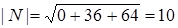 Þ
Þ 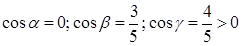
2. 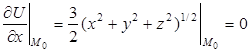

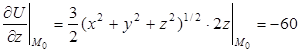
3. 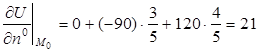
2. Градиент скалярного поля.
Определение: Градиентом скалярной функции U=U(x,y,z) в точке 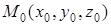 называется вектор
называется вектор
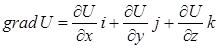
выходящий из точки 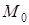 и указывающий направление наибыстрейшего роста функции U.
и указывающий направление наибыстрейшего роста функции U.
Определение: Градиент функции и производная в направлении связаны соотношением:
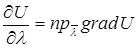
Задача. Найти точки, в которых функция 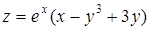 стационарна (т.е. точки, в которых производная по любому направлению равнялась нулю).
стационарна (т.е. точки, в которых производная по любому направлению равнялась нулю).
1. 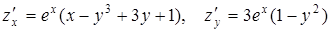
2. Необходимо и достаточно, что бы все частные производные первого порядка в данных точках равнялись нулю, т.е. 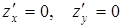 функция стационарна в точках
функция стационарна в точках 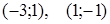 .
.
Задача. Найти угол между градиентами скалярных полей 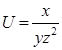 и
и 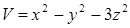 в точке
в точке 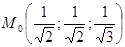 .
.
1. 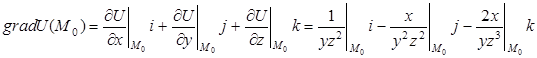
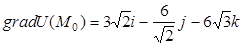
2. 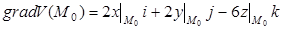
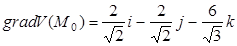
3. 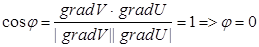
Ответ: 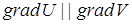
3. Векторные линии.
Определение: Векторной линией называется линия, касательная к которой в каждой точке совпадает с направлением векторного поля 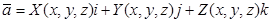 и определяются они системой дифференциальных уравнений:
и определяются они системой дифференциальных уравнений:
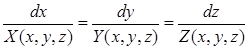
Задача. Найти векторные линии в векторном поле 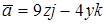 .
.
1. Из 
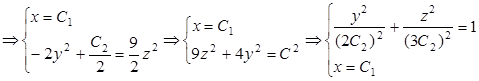
Векторными линиями данного поля будут эллипсы расположенные в плоскостях перпендикулярных оси Ох.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|