Правильные пирамиды (Sполн=Sосн+Sбок; V=1/3•Sосн•H)

План дистанционного обучения учащихся 9 А ,Б классов по геометрии на период с 13.04.2020 по 17.04.2020 Учитель Хотякова И.В. учитель Хотякова И.В. атериалы к дистанционному уроку по математике в 9 классах

Номер

урока

Класс

Дата проведения

Тема

Задание

контроль

9-А 9-Б

15.04.2020

Решение задач практического содержания

Тема «Построения в стереометрии» одна из основных в традиционном курсе школьной геометрии. Она составляет, можно сказать, центральный предмет стереометрии. В дальнейшем построения широко используется в строительном деле, архитектуре, машиностроении, геодезии, во многих других областях науки и техники. Метод следов. Суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры. Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют следом секущей плоскости. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры. Последовательно соединяя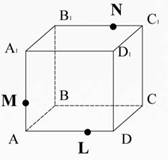

образы этих точек, получим изображение искомого сечения. Примеры построения сечений. Пример 1. Рассмотрим прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Построим сечение, проходящее через точки M, N, L (Рис. 23). Рис. 23 Соединим точки M и L, лежащие в плоскости AA₁D₁D (Рис. 24).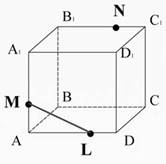

Рис. 24

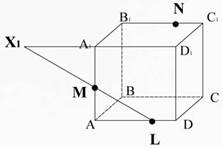Пересечем прямую ML (принадлежащую сечению) с ребром A₁D₁, они лежат в одной плоскости AA₁D₁D. Получим точку X₁ (Рис. 25). Рис. 25

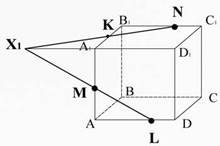Точка X₁ лежит на ребре A₁D₁, а значит и плоскости A₁B₁C₁D₁, соединим ее с точкой N, лежащей в этой же плоскости (Рис. 26) X₁N пересекается с ребром A₁B₁ в точке К. Рис. 26 Соединим точки K и M, лежащие в одной плоскости AA₁B₁B (Рис. 27).

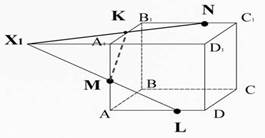Рис. 27

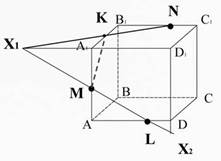Найдем прямую пересечения плоскости сечения с плоскостью DD₁C₁C: пересечем прямую ML (принадлежащую сечению) с ребром DD₁, они лежат в одной плоскости AA₁D₁D, получим точку X₂ (Рис.28); Рис. 28 Пересечем прямую KN (принадлежащую сечению) с ребром D₁C₁, они лежат в одной плоскости A₁B₁C₁D₁, получим точку X₃ (Рис. 29);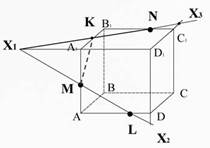

Рис. 29 Точки X₂ и X₃лежат в плоскости DD₁C₁C. Проведем прямую X₂ X₃ , которая пересечет ребро C₁C в точке T, а ребро DC в точке P. И соединим точки L и P, лежащие в плоскости ABCD (Рис. 30) MKNTPL - искомое сечение.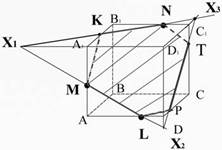

Рис. 30 Пример 2 Дано: Построить сечение призмы ABCDA₁B₁C₁D₁ – призма, M ϵ A₁B₁, N ϵ AD, P ϵ DC Найти: Сечение ABCDA₁B₁C₁D₁ плоскостью проходящей через точки M, N, P Решение: Точки N и P лежат в плоскости сечения и в плоскости нижнего основания параллелепипеда. Построим прямую, проходящую через эти точки. Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда. Продолжим прямую, на которой лежит сторона AB параллелепипеда. Прямые AB и NP пересекутся в некоторой точке S. Эта точка принадлежит плоскости сечения. Так как точка M также принадлежит плоскости сечения и пересекает прямую АА₁ в некоторой точке Х. Точки X и N лежат в одной плоскости грани АА₁D₁D, соединим их и получим прямую XN. Так как плоскости граней параллелепипеда параллельны, то через точку M можно провести прямую в грани A₁B₁C₁D₁, параллельную прямой NP. Эта прямая пересечет сторону В₁С₁ в точке Y. Аналогично проводим прямую YZ, параллельно прямой XN. Соединяем Z с P и получаем искомое сечение – MYZPNX. 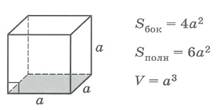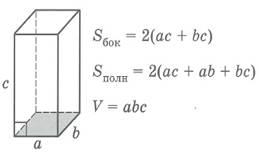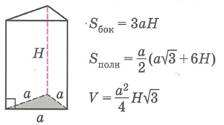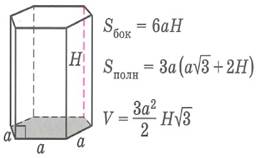Основные формулы объемов и площадей поверхностей многогранников и тел вращения


Куб		Прямоугольный параллелепипед
Правильная треугольная призма		Правильная шестиугольная призма

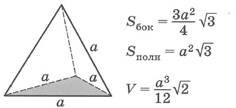
Правильные пирамиды (Sполн=Sосн+Sбок; V=1/3•Sосн•H)

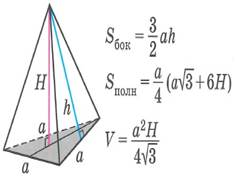
Тертраэдр

Правильная треугольная пирамида

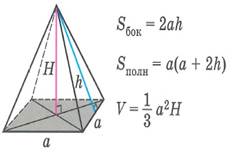
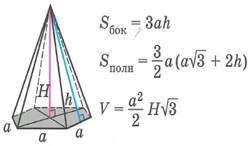
Правильная четырехугольная пирамида

Правильная шестиугольная пирамида

S_бок- площадь боковой поверхности многогранника, S_полн - площадь полной поверхности многогранника, S_осн - площадь основания многогранника, V - объем многогранника.

12 Следующая ⇒