Законы алгебры логики. Переместительный (коммутативный) закон. Сочетательный (ассоциативный) закон. Распределительный (дистрибутивный) закон. Закон двойного отрицания. Закон исключения третьего. Закон повторения. Законы операций с 0 и 1. Закон поглощения

Законы алгебры логики

Многие законы алгебры логики аналогичны законам алгебры. В то же время есть законы, которые присущи только ей. Надо помнить, что под переменными здесь подразумеваются высказывания. Поэтому в алгебре логики не может быть коэффициентов и степеней. Ведь сколько раз не повторяй, что вода мокрая, мокрей она не станет.

1. Переместительный (коммутативный) закон

o для конъюнкции:

А * В = В * А;

o для дизъюнкции:

A ∨ B = В ∨ А.

2. Сочетательный (ассоциативный) закон

o для конъюнкции:

(А * В) * С = А * (B * С);

o для дизъюнкции:

(A ∨ B) ∨ C = A ∨(B ∨ C).

При одинаковых знаках операций скобки можно ставить произвольно или вообще опускать.

3. Распределительный (дистрибутивный) закон

o для конъюнкции:

А * (В ∨ С) = (А * В) ∨ (А * С);

o для дизъюнкции:

A ∨ (B * С) = (A ∨ В) * (A ∨ С).

4. Закон двойного отрицания

Двойное отрицание исключает отрицание.

5. Закон исключения третьего

Из двух противоречивых высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.

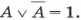
Невозможно, чтобы противоречивые высказывания были одновременно истинными.

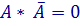
6. Закон повторения

o для конъюнкции:

А * А = А;

o для дизъюнкции:

A ∨ А = А.

7. Законы операций с 0 и 1

o для конъюнкции:

А * 0 = 0; А * 1 = А;

o для дизъюнкции:

A ∨ O = A; A ∨ l = l.

8. Закон поглощения

o для конъюнкции:

А * (A V B) = A

o для дизъюнкции:

A V (A * B) = A

12 Следующая ⇒