Осевая симметрия — это симметрия относительно проведённой прямой (оси).

Осевая симметрия — это симметрия относительно проведённой прямой (оси).

Точки M и M1 симметричны относительно некоторой прямой (оси симметрии), если эти точки лежат на прямой, перпендикулярной данной, и на одинаковом расстоянии от оси симметрии.

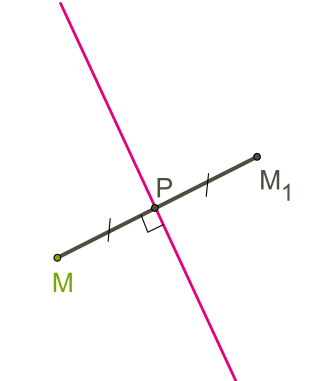
Алгоритм построения фигуры, симметричной относительно некоторой прямой.

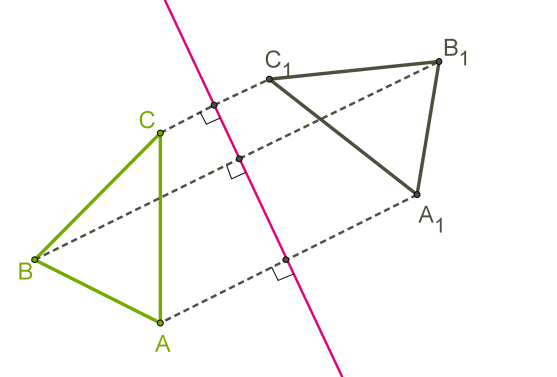
Построим треугольник A1B1C1, симметричный треугольнику ABC относительно красной прямой:

1. для этого проведём из вершин треугольника ABC прямые, перпендикулярные оси симметрии, и продолжим их дальше на другой стороне оси.
2. Измерим расстояния от вершин треугольника до получившихся точек на прямой и отложим с другой стороны прямой такие же расстояния.
3. Соединим получившиеся точки отрезками и получим треугольник A1B1C1, симметричный данному треугольнику ABC.

Фигуры, симметричные относительно прямой, равны.

Фигура считается симметричной относительно прямой, если для каждой точки рассматриваемой фигуры симметричная для неё точка относительно данной прямой также находится на этой фигуре. Прямая является в этом случае осью симметрии фигуры.

Иногда у фигур несколько осей симметрии:

· для неразвёрнутого угла существует единственная ось симметрии — это биссектриса данного угла.

· Для равнобедренного треугольника есть единственная ось симметрии.

· Для равностороннего треугольника — три оси.

· Для прямоугольника и ромба существуют две оси симметрии.

· Для квадрата — целых четыре.

· Для окружности осей симметрии бесчисленное множество — это каждая прямая, которая проходит через центр этой фигуры.

· Есть фигуры без осей симметрии — это параллелограмм и треугольник, все стороны которого различны.

⇐ Предыдущая 12