Симметрию относительно точки называют центральной симметрией.

Осевая и центральная симметрия.

Теория:

Симметрия — слово греческого происхождения, как и многие другие слова, которые связаны с математикой. Оно означает соразмерность, наличие определённого порядка, закономерности в расположении частей. Смотря на объекты вокруг, мы не раз восклицаем: «Какая симметрия!»

Люди с давних времён использовали симметрию в рисунках, орнаментах, предметах быта, в архитектуре, художестве, строительстве.

Но симметрия широко распространена и в природе, где не было вмешательства человеческой руки. Её можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных, в форме кристаллических тел, в порхающей бабочке, загадочной снежинке, морской звезде.

Пока рассмотрим две симметрии на плоскости: относительно точки и прямой.

Центральная симметрия

Симметрию относительно точки называют центральной симметрией.

Точки M и M1 симметричны относительно некоторой точки O, если точка O является серединой отрезка MM1.

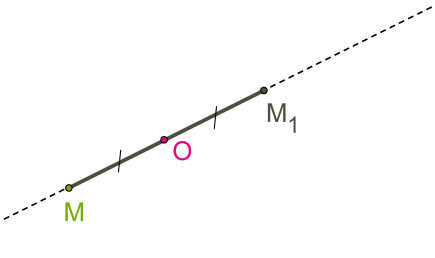
Точка O называется центром симметрии.

Алгоритм построения центрально-симметричных фигур.

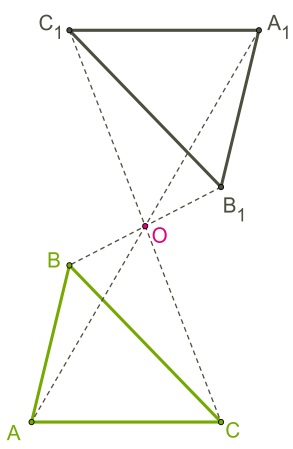
Построим треугольник A1B1C1, симметричный треугольнику ABC относительно центра (точки) O:

1. для этого соединим точки A, B, C с центром O и продолжим эти отрезки;
2. измерим отрезки AO, BO, CO и отложим с другой стороны от точки O равные им отрезки AO=OA1;BO=OB1;CO=OC1;
3. соединим получившиеся точки отрезками и получим треугольник A1B1C1, симметричный данному треугольнику ABC.

Фигуры, симметричные относительно некоторой точки, равны.

Фигура симметрична относительно центра симметрии, если для каждой этой точки фигуры симметричная ей точка также лежит на этой фигуре. Такая фигура имеет центр симметрии (фигура с центральной симметрией).

Есть фигуры с центральной симметрией, это, например, окружность и параллелограмм. У окружности центр симметрии — это её центр, у параллелограмма центр симметрии — это точка, в которой пересекаются его диагонали. Есть очень много фигур, у которых нет центра симметрии.

Осевая симметрия

12 Следующая ⇒