
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ПРАКТИЧЕСКАЯ ТЕТРАДЬ. по теме «Первообразная и интеграл». Тема: ПЕРВООБРАЗНАЯ. ИНТЕГРАЛ. СПРАВОЧНЫЙ МАТЕРИАЛ. УПРАЖНЕНИЯ С РЕШЕНИИЯМИ
ПРАКТИЧЕСКАЯ ТЕТРАДЬ
по теме «Первообразная и интеграл»
Тема: ПЕРВООБРАЗНАЯ. ИНТЕГРАЛ
СПРАВОЧНЫЙ МАТЕРИАЛ
Определение.Если для любого 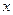 из множества Х выполняется равенство
из множества Х выполняется равенство 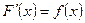 , то функцию
, то функцию 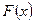 называют первообразной для функции
называют первообразной для функции 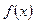 на данном промежутке.
на данном промежутке.
Функция
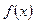
| Первообразная 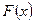
| Функция
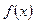
| Первообразная 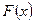
|
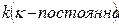
| 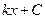
| 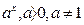
| 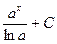
|

| 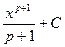
| 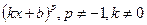
| 
|

| 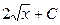
| 
| 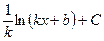
|
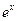
| 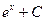
| 
| 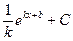
|
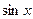
| 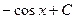
| 
| 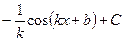
|
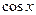
| 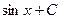
| 
| 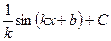
|
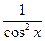
| 
| 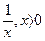
| 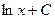
|
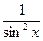
| 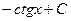
|
Криволинейной трапецией называют,фигуру ограниченную графиком этой функции, отрезком [a;b] и прямыми  и
и  .
.
Формула нахождения неопределенного интеграла:
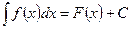
Формула Ньютона –Лейбница:
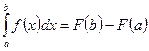
Формула вычисления площади криволинейной трапеции: 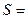
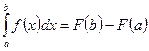
Формула вычисления объема тела вращения:
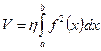
| Правила нахождения первообразных | Правила нахождения интеграла. |
Постоянный множитель можно вынести за знак производной:
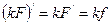 где где 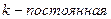 , ,
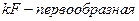 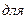  . .
|
Постоянный множитель можно вынести за знак интеграла:
 где где 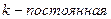
|
Производная суммы

|
Интеграл от суммы равен сумме интегралов;
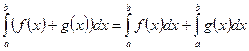
|
Производная сложной функции
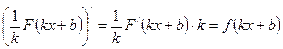
|
Формула замены переменной:
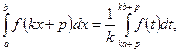 где где 
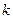 и и 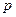 - постоянные - постоянные
|
УПРАЖНЕНИЯ С РЕШЕНИИЯМИ
Пример1. Вычислите интеграл: 
Решение: Одной из первообразных для подынтегральной функции будет  . Следовательно, имеем
. Следовательно, имеем  .
.
Пример2. Найти одну из первообразных функции 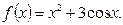
Решение:Используя, правила интегрирования и таблицу первообразных для функции  при
при 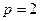 и для
и для 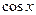 ,находим одну из первообразных данной функции:
,находим одну из первообразных данной функции:
Ответ:  .
.
Пример 3. Для функции 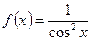 найти первообразную, график которой проходит через точку
найти первообразную, график которой проходит через точку 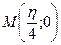 .
.
Решение: Общим видом первообразных для 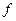 является функция
является функция 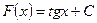 .Решая уравнение:
.Решая уравнение: 
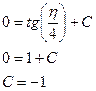
Таким образом ,искомая первообразная есть функция
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|