
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Понятие об итерационных методах решения СЛАУ.
1. Понятие об итерационных методах решения СЛАУ.
В отличие от прямых методов, итерационные методы обычно не дают точного ответа за конечное число шагов, однако на каждом шаге уменьшают ошибку на какую-то долю. Итерации прекращают, когда ошибка становится меньше допуска, заданного вычислителем (пользователем). Величина финальной ошибки зависит от количества итераций, а также от свойств метода и СЛАУ. Другими словам, итерационные методы дают решение СЛАУ в виде предела последовательности некоторых векторов, построение которых осуществляется посредством единообразного процесса, называемого итерационным процессом.
Рассмотрим два простейших итерационных метода решения СЛАУ – метод простой итерации и метод Зейделя.
Пусть требуется решить СЛАУ
 (1)
(1)
Итерационные методы решения системы уравнений (1) состоят в построении последовательности векторов
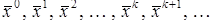 (2)
(2)
по некоторому алгоритму, такому, что из 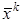 следует
следует  . При этом
. При этом
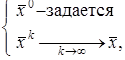 (3)
(3)
где 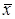 – точное решение системы, а
– точное решение системы, а 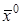 – называется начальным приближением решения.
– называется начальным приближением решения.
Вычисления ведутся до тех пор, пока норма разницы двух последовательных приближений не станет
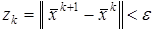 , (4)
, (4)
где e – малое положительное число (заданная точность). С точностью до e решение принимается равным 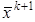 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|