Хелпикс

Главная

Контакты

Случайная статья



Практическая работа № 4. Задание 3.

⇐ ПредыдущаяСтр 4 из 4


Практическая работа № 4

Тема. Элементы теории вероятностей. Дискретная и непрерывная случайные величины. Закон распределения случайной величины. По заданному условию построить закон распределения дискретной случайной величины.

Цель работы:                      

Используя теоретический материал и образцы решения, закрепить навыки решения задач по теме «Элементы теории вероятностей. Дискретная и непрерывная случайные величины. Закон распределения случайной величины. По заданному условию построить закон распределения дискретной случайной величины»

 

 Приложение

Задание 1. Задает ли закон распределения дискретной случайной величины данная таблица

В1

X
P 0,1 0,2 0,25 0,17 0,3

В2   

X
P 0,11 0,19 0,2 0,2 0,3

В3

X
P 0,13 0,17 0,3 0,37 0,68

В4

X
P 0,2 0,3 0,11 0,13 0,47

В5

X
P 0,1 0,2 0,25 0,17 0,3

В6   

X
P 0,11 0,19 0,2 0,2 0,3

В7

X
P 0,13 0,17 0,3 0,37 0,68

 

В8

X
P 0,2 0,3 0,11 0,13 0,47

В9

X
P 0,1 0,2 0,25 0,17 0,3

В10

X
P 0,2 0,3 0,11 0,13 0,47

Задание 2. Дискретная случайная величина имеет закон распределения. Найти неизвестную вероятность.

В1

X
P 0,13 0,3 0,2 P4 0,17

В2

X
P 0,15 0,16 P3 0,5 0,07

В3

X
P 0,3 P2 0,2 0,29 0,1

В4

X
P 0,16 P2 0,15 0,07 0,5

В5

X
P 0,13 0,3 0,2 P4 0,17

В6

X
P 0,15 0,16 P3 0,5 0,07

В7

X
P 0,3 P2 0,2 0,29 0,1

В8

X
P 0,13 0,3 0,2 P4 0,17

В9

X
P 0,15 0,16 P3 0,5 0,07

В10

X
P 0,13 0,3 0,2 P4 0,17

Задание 3.

В1. Из 40 вопросов, входящих в экзаменационные билеты, студент знает 30. Найти вероятность того, что среди трех наугад выбранных вопросов студент знает 2 вопроса.
В2. В лотерее разыгрывается 100 билетов. Выигрыши выпали на 20 билетов. Некто приобрел 5 билетов. Найти вероятность того, что выигрыш выпадет хотя бы на один билет.
В3.Какова вероятность того, что два определенных студента будут посланы на практику в город С, если в наличии имеется 5 мест в город А, 8- в город В и 7 – в город С.
В4. Один студент выучил 20 из 25 вопросов программы по математике, а второй - только 15. каждому из них задают по одному вопросу. Найти вероятность того, что правильно ответит только первый студент.
В5. Из букв А, А, И, Л, М, Н разрезной азбуки выбирают наудачу по одной и ставят в ряд. Найти вероятность того, что получится слово: МИНА.
В6. В ящике содержаться 9 белых , 6 черных и 5 зеленых шаров. Наудачу вынимается один шар. Найти вероятность того, что он окажется либо черным, либо зеленым.
В7. В ящике находится 20 деталей, 4 из них – нестандартные. Какова вероятность того, что среди 6 наугад взятых деталей нестандартных не окажется?
В8. В группе 10 юношей и 10 девушек. Для дежурства путем жеребьевки выделяют 5 человек. Какова вероятность того, что в число дежурных войдут 2 юношей и 3 девушки?
В9. Три стрелка делают по одному выстрелу в цель. Вероятности попаданий в цель соответственно равны 0,6; 0,85; 0,7. Какова вероятность попадания в цель только второго стрелка?
В10. Один студент выучил 30 из 35 вопросов программы по математике, а второй - только 15. каждому из них задают по одному вопросу. Найти вероятность того, что правильно ответит только первый студент.

Задание 4.

Вариант1

1. Случайная величина X распределена по закону:

 –1

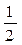
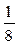
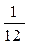
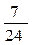
Найдите математическое ожидание и дисперсию случайной величины X.

2. В лотерее разыгрывается 20000 билетов. Найдите математическое ожидание и дисперсию числа выигрышных билетов, если каждый билет может выигрышным с вероятностью 0,3.

Вариант 2

1. Случайная величина X распределена по закону:

 0

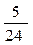
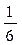
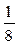
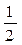
Найдите математическое ожидание и дисперсию случайной величины X.

2. В магазин поступила партия из 50 коробок с обувью черного и коричневого цвета. Найдите математическое ожидание и дисперсию числа коробок с обувью коричневого цвета, если вероятность того, что обувь будет коричневого цвета равна 0,2.

Вариант 3

1. Случайная величина X распределена по закону:

 –1

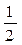
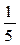
Найдите математическое ожидание и дисперсию случайной величины X.

2. Найдите математическое ожидание и дисперсию числа не взошедших семян из 800 посеянных семян данного растения, если каждое из семян может не взойти с вероятностью 0,01.

Вариант 4

1. Случайная величина X распределена по закону:

 –1
0,1 0,2 0,3 0,4

Найдите математическое ожидание и дисперсию случайной величины X.

2. Найдите математическое ожидание и дисперсию числа студентов, которые не сдадут экзамен, в группе из 30 человек, если каждый студент может не сдать экзамен с вероятностью 0,4.

Вариант 5

1. Случайная величина X распределена по закону:

 –2 –1
0,2 0,1 0,2 0,5

Найдите математическое ожидание и дисперсию случайной величины X.

2. В урне находятся всего 100 белых и чёрных шаров. Найдите математическое ожидание и дисперсию числа белых шаров, если вероятность того, что шар будет белым равна 0,02.

Вариант 6

1. Случайная величина X распределена по закону:

 1
0,07 0,03 0,9

Найдите математическое ожидание и дисперсию случайной величины X.

2. Найдите математическое ожидание и дисперсию числа нестандартных ламп в партии из 300 ламп, если каждая лампа может оказаться нестандартной с вероятностью 0,07.

Вариант 7

1. Случайная величина X распределена по закону:

 –1

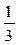
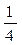
Найдите математическое ожидание и дисперсию случайной величины X.

2. Найдите математическое ожидание и дисперсию числа фальшивых билетов, купленных на самолёт, в партии из 150 билетов, если каждый билет может оказаться фальшивым с вероятностью 0,004.

Вариант 8

1. Случайная величина X распределена по закону:

0,4 0,5 0,1

Найдите математическое ожидание и дисперсию случайной величины X.

2. Найдите математическое ожидание и дисперсию числа изделий со знаком качества в партии из 7000 деталей, если каждая деталь может оказаться со знаком качества с вероятностью 0,8.

Вариант 9

1. Случайная величина X распределена по закону:

 –1

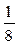
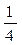
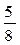
Найдите математическое ожидание и дисперсию случайной величины X.

2. Найдите математическое ожидание и дисперсию числа поддельных медицинских препаратов в партии из 126 препаратов, если каждый препарат может быть поддельным с вероятностью 0,06.

 

Вариант 10

1. Случайная величина X распределена по закону:

 –2 –1
0,2 0,1 0,2 0,5

Найдите математическое ожидание и дисперсию случайной величины X.

2. В урне находятся всего 100 белых и чёрных шаров. Найдите математическое ожидание и дисперсию числа белых шаров, если вероятность того, что шар будет белым равна 0,03.

 

 


⇐ Предыдущая1234
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.