Контакты

Случайная статья

Решите уравнение Если уравнение имеет более одного корня, в ответе укажите меньший из них.

⇐ ПредыдущаяСтр 2 из 2

Решение.

Последовательно получаем:

Ответ: 2.

4. Найдите корень уравнения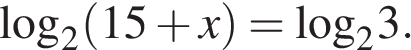

Решение.

Последовательно получаем:

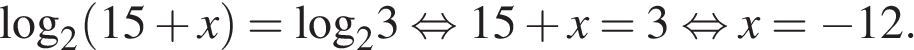
Ответ: −12.

5. Найдите корень уравнения

Решение.

Логарифмы двух выражений равны, если сами выражения равны и при этом положительны:

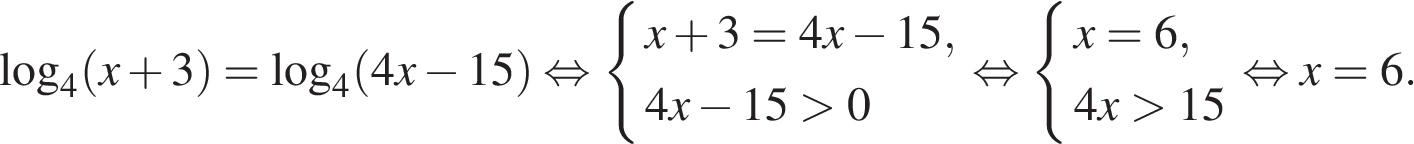
Ответ: 6.

6. Найдите корень уравнения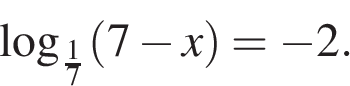

Решение.

Последовательно получаем:

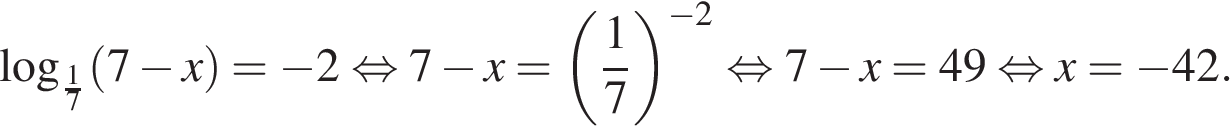
Ответ: −42.

7. Найдите корень уравнения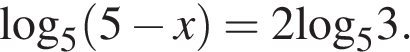

Решение.

Последовательно получаем:

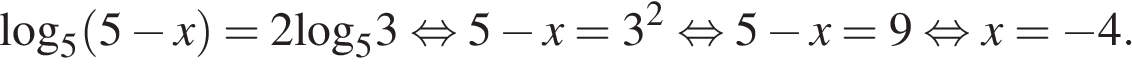
Ответ: −4.

8. Решите уравнение

Решение.

Перейдем к одному основанию степени:

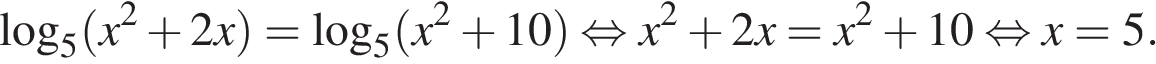
Ответ: 5.

9. Решите уравнение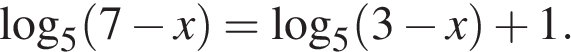

Решение.

Заметим, что 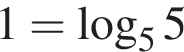и используем формулу 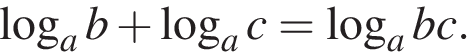Имеем:

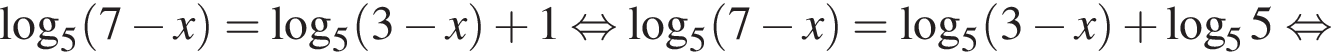
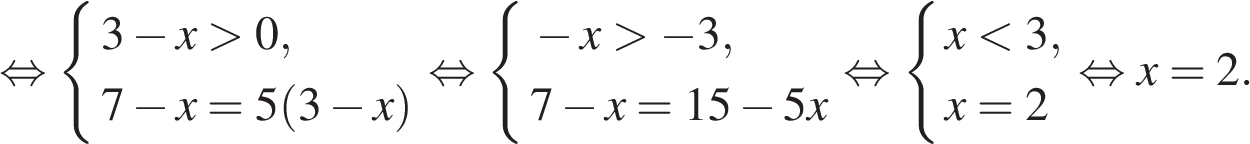
Ответ: 2.

10. Решите уравнение Если уравнение имеет более одного корня, в ответе укажите меньший из них.

Решение.

На ОДЗ перейдем к уравнению на основание логарифма:

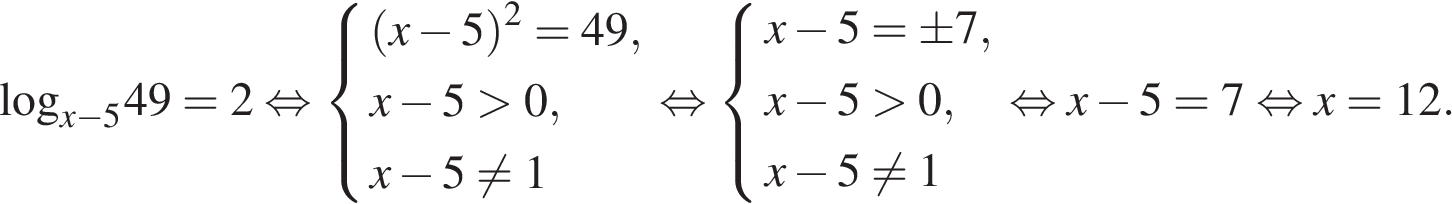
Итак, на ОДЗ уравнение имеет только один корень.

Ответ: 12.

11. Найдите корень уравнения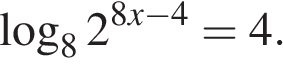

Решение.

Используем формулу :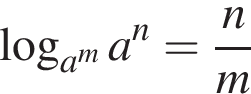

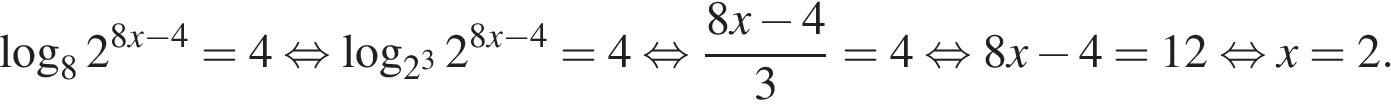
Приведем другое решение:

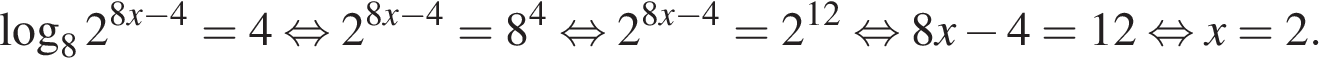
Ответ:2.

12. Найдите корень уравнения

Решение.

Используя формулу , получаем:

Ответ: 13,4.

Примечание.

Следует отличать это уравнение от похожего, но другого: 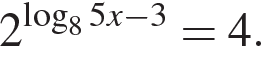В этом случае имеем:

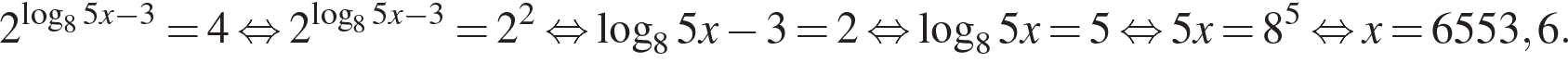
13. Найдите корень уравнения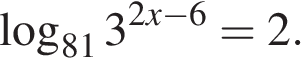

Решение.

Последовательно решаем уравнение:

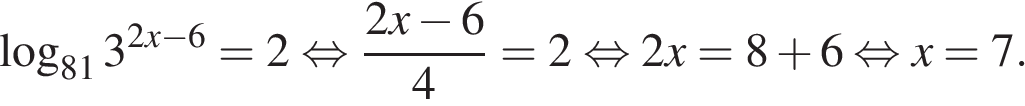
Ответ: 7.

14. Найдите корень уравнения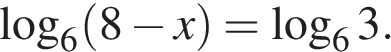

Решение.

Последовательно получаем:

Ответ: 5.

15. Найдите корень уравнения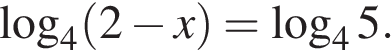

Решение.

Последовательно получаем:

Ответ: −3.

16. Решите уравнение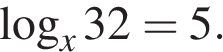

Решение.

На ОДЗ перейдем к уравнению на основание логарифма:

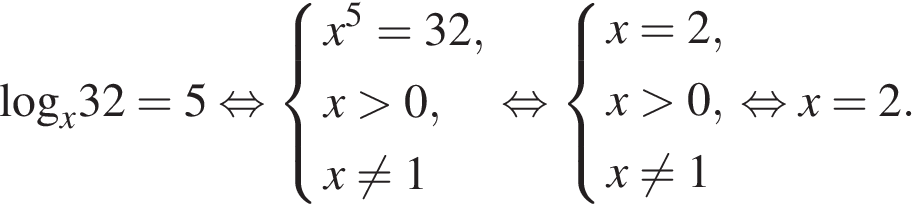
Итак, на ОДЗ уравнение имеет только один корень.

Ответ: 2.

⇐ Предыдущая 12

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.