
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение.. Решение.. Ответ: Р(А) ≈ 0,496. Решение.. Решение.
Решение.
Поскольку в условиях независимых испытаний Бернулли вероятность р = 0,01 близка к нулю, а n = 500 велико, применим формулу Пуассона:
Pn(k) = 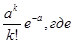 a=500 ∙ 0,01 = 5
a=500 ∙ 0,01 = 5
Для k = 0 (отсутствие опечаток), получаем: H500(0) = 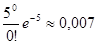
Ответ: Р500 ≈ 0,007
4. Узел содержит три независимо работающие детали. Вероятность отказа деталей соответственно равны 0,1; 0,2; 0,3. Найти вероятность отказа учла, если для этого достаточно, чтобы отказала хотя бы одна деталь.
Решение.
Для нахождения вероятности события А - отказа узла, найдем сначала вероятность противоположного события Р(Ā), заключающегося в исправной работе всех деталей:
Р(Ā) = (1-0,1)∙(1-0,2)∙(1-0,3) = 0,9∙0,8∙0,7 = 0,504.
Искомая вероятность равна:
Р(А) = 1 - Р(Ā) = 1-0,504 = 0,496
Ответ: Р(А) ≈ 0,496
5. Монета бросается пять раз. Найти вероятность того, что орел выпадет 2 раза.
Решение.
По формуле Бернулли при n = 5, р = 0,5 найдем искомую вероятность:
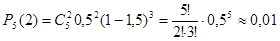
Ответ: Р2(2) ≈ 0,01
6. Два завода производят детали, поступающие в магазин. Вероятность выпуска бракованной детали для первого завода равна 0,8, для второго - 0,7. С первого завода поступило в 3 раза больше деталей, чем со второго. Покупатель приобрел годную деталь. Найти вероятность того, что она с первого завода.
Решение.
Этот пример решим по формуле Байеса:
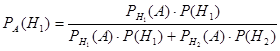
Где события (гипотезы) Н1 и Н2 - произвольно выбранная соответственно первом или втором заводе деталь; событие А заключается в том, что деталь годная. Получим:
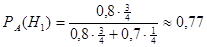
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|