Контакты

Случайная статья

Обратная матрица. Задачи.

⇐ ПредыдущаяСтр 2 из 2

Обратная матрица

Определение 1. Пусть A – квадратная матрица n–го порядка, а E – единичная матрица того же порядка. Матрица A^–1 называется обратной по отношению к матрице A, если выполняются равенства: A×A^–1= A^–1×A=E.

Определение 2. Минором какого-либо элемента определителя называется определитель, полученный из данного вычёркиванием той строки и того столбца, которым принадлежит этот элемент.

Минор элемента a_ik определителя 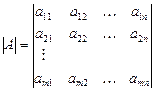обозначается M_ik.

Пример 1. Минор M₁₂ определителя 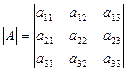равен .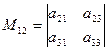

Определение 3. Алгебраическим дополнением A_ik элемента a_ik определителя 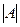называется его минор M_ik, взятый со знаком 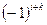. Следовательно, .

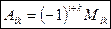Пример 2. Алгебраическое дополнение A₁₂ определителя 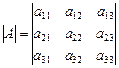равно .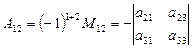

Теорема. Матрица ,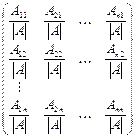

где A_ik – алгебраическое дополнение элемента a_ik невырожденной матрицы A, является обратной для A.

Для матрицы 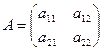обратной является матрица .

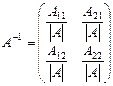Пример 3. Дана матрица . Найдите обратную матрицу.

, , , , .

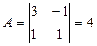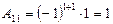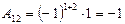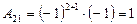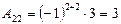Тогда 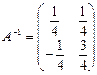. Сделаем проверку: .

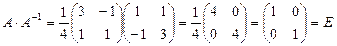Задачи.

1. Дана матрица 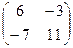. Тогда алгебраическим дополнением элемента 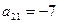является

1) -3 2) 6 3) -7 4) 3

2. Дана матрица 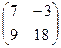. Тогда алгебраическим дополнением элемента 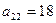является

1) 18 2) 7 3) -3 4) 9

3. Дана матрица . Тогда алгебраическим дополнением элемента 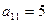является

1) 16 2) 11 3) -16 4) 5

4. Дана матрица . Тогда алгебраическим дополнением элемента является

1) 9 2) -9 3) 1 4) -7

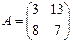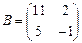5. Если и , то матрица C=A-3B имеет вид …

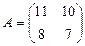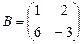6. Если и , то матрица C=A+B имеет вид …

7. Если 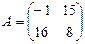и , то матрица C=A+3B имеет вид …

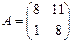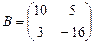8. Если и , то матрица C=A+5B имеет вид …

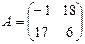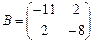9. Если и , то матрица C=A-B имеет вид …

10. Если 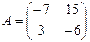, , то матрица 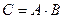имеет вид …

11. Если 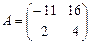, , 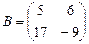то матрица 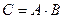имеет вид …

12. Если 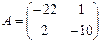, , 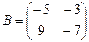то матрица 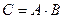имеет вид …

13. Если 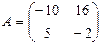, , 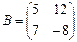то матрица 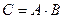имеет вид …

14. Если 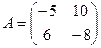, , 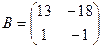то матрица 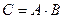имеет вид…

15. Найдите обратную матрицу для матриц: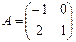

.

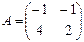
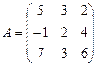
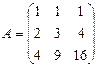
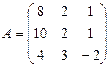
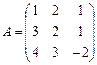⇐ Предыдущая 12

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.