
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема 2. Матрицы и действия над ними
Тема 2. Матрицы и действия над ними
Основные определения
Определение 1. Матрицей называется таблица чисел aik вида: 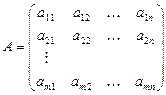
состоящая из m строк и n столбцов. Числа aik называются её элементами. Это прямоугольная матрица. В частности, если m=1, n>1, получаем матрицу-строку 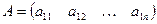 , а если m>1, n=1, матрицу-столбец:
, а если m>1, n=1, матрицу-столбец: 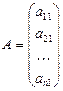 .
.
Определение 2. Матрица 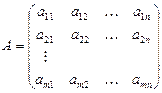 называется невырожденной (неособой), если её определитель
называется невырожденной (неособой), если её определитель 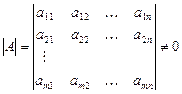 и вырожденной (особой), если
и вырожденной (особой), если 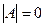 .
.
Определение 3. Матрица называется квадратной, если m=n (n – порядок матрицы). В частности, матрица 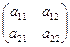 называется квадратной матрицей второго порядка, а матрица
называется квадратной матрицей второго порядка, а матрица 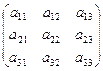 - квадратной матрицей третьего порядка.
- квадратной матрицей третьего порядка.
Определение 4. Квадратная матрица называется диагональной, если все элементы, стоящие вне главной диагонали равны нулю: aij =0 i¹j.

В частности, диагональная матрица, у которой все диагональные элементы равны единице называется единичной. 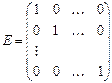
Определение 5. Нулевой матрицей называется матрица, все элементы которой равны нулю:
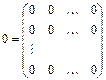
Действия над матрицами
Определение 1. Две матрицы A и B называются равными, если они одинакового размера (т.е. имеют одинаковое число строк и одинаковое число столбцов) и их соответствующие элементы равны. В частности, если
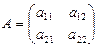 и
и 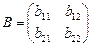
и A=B, то a11=b11, a12=b12, a21=b21, a22=b22.
Матрицы одинакового размера можно складывать и вычитать.
Определение 2. Суммой двух матриц A и B называется матрица С, элементы которой равны сумме соответствующих элементов матриц A и B (обозначение C=A+B). В частности, для квадратных матриц второго порядка получаем:
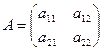 ,
, 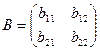 ,
, 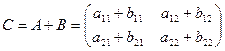 .
.
Пример 1. Найдите сумму матриц 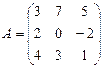 и
и 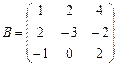 .
.
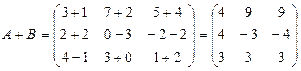
Сумма нулевой матрицы и любой матрицы A даёт матрицу A: A+0 = A.
Определение 3. Разностью двух матриц A и B называется матрица С, элементы которой равны разности соответствующих элементов матриц A и B (обозначение C=A+B).
Пример 2. Найдите разность матриц 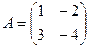 и
и 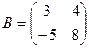 .
.
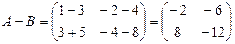 .
.
Определение 4. Произведение матрицы A на число a называется матрица, элементы которой получаются из соответствующих элементов матрицы А умножением на число a.
Пример 3. Найдите матрицу 3A+5B, если 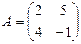 ,
, 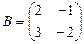 .
.
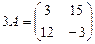 ,
, 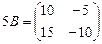 ,
, 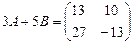 .
.
Определение 5. Произведение матриц А×В определено в том и только в том случае, если число столбцов матрицы А равно числу строк матрицы В. Произведение матрицы А размера m´k на матрицу B размера k´n называется матрица C=A×B размера m´n, элементы которой определяются по формуле: 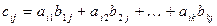
Данная сумма представляет собой сумму произведений соответствующих элементов строки i матрицы А и столбца j матрицы В.
Рассмотрим правило умножения квадратных матриц второго порядка. Пусть даны две матрицы: 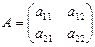 и
и 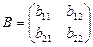 .
.
Произведением матрицы A на матрицу B называется матрица C=AB, равная:
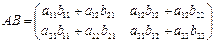 .
.
Пример 4. Найдите произведение A·B и B·A матриц 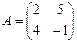 и
и 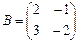 .
.
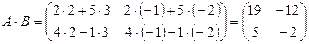
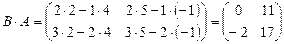
Пример 5. 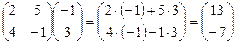
По отношению к произведению двух матриц переместительный закон не выполняется, т.е. A·B ≠ B·A.
Произведение единичной матрицы и любой матрицы A даёт матрицу A: EA = AE=A.
Определение 6. Матрица AT полученная из матрицы А заменой строк столбцами, называется транспонированной.
Пример 6. 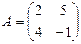 ,
, 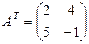 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|