- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Однородные тригонометрические уравнения
⇐ ПредыдущаяСтр 2 из 2
Однородные тригонометрические уравнения
sin2x + 2sinxcosx – 3 cos2x = 0
Сумма показателей степеней синуса и косинуса в каждом слагаемом одна и та же (в нашем примере равна 2), свободный член в уравнении отсутствует, т.е. равен 0. Такое уравнение называется однородным относительно sinx и cosx, а число 2 – порядком его однородности.
Разделим все члены данного уравнения на cos2x ≠ 0, получим:
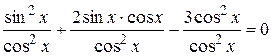
tg2x + 2tgx – 3 = 0
tgx = y
y2 + 2y – 3 = 0
y = 1; y = –3
tgx = 1
x =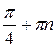 
, n 
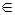Z
tg x = –3
x = arctg (–3) + πn, n 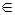Z
Ответ: 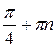, arctg (–3) + πn, n 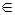Z
Реши сам:
1) sinx + cosx = 0
2) 
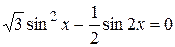
3) sin2x + 0,5sin2x – 2cos2x = 0
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|