Теорема умножения вероятностей

Теорема умножения вероятностей

Теорема. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место

P(AB) = P(A)×P(B/A) = P(B)×P(A/B).

Пример. На склад поступило 35 холодильников. Известно, что 5 холодильников с дефектами, но неизвестно, какие это холодильники. Найти вероятность того, что два взятых наугад холодильника будут с дефектами.

Решение. Вероятность того, что первый выбранный холодильник будет с дефектом, находится как отношение числа благоприятствующих исходов к общему числу возможных исходов

P(A) = 5/35 = 1/7.

Но после того, как был взят первый холодильник с дефектом, условная вероятность того, что и второй будет с дефектом, определяется на основе соотношения

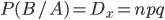
Искомая вероятность будет

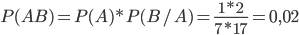Теорема сложения вероятностей совместных событий

Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же опыте.

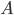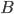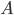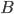Пример. Поступление в магазин одного вида товара — событие . Поступление второго вида товара — событие . Поступить эти товары могут и одновременно. Поэтому и - совместные события.

Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления

P(A+B) = P(A) + P(B) — P(AB).

Пример. Если вероятность поступления в магазин одного вида товара равна P(A) = 0,4, а второго товара — P(B) = 0,5, и если допустить, что эти события независимы, но совместны, то вероятность суммы событий равна

P(A+B) = 0,4 + 0,5 — 0,4×0,5 = 0,7.

⇐ Предыдущая 12