
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Зачет по контрольной работе и наличие лекций является допуском к экзамену!
Зачет по контрольной работе и наличие лекций является допуском к экзамену!
Контрольная работа по математике
1. Найти ранг матрицы
1.1 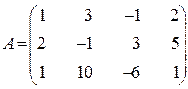 .
.
1.2 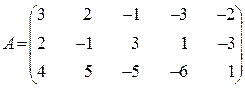 .
.
1.3 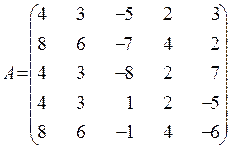
1.4 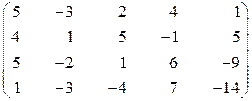
1.5 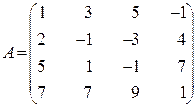
1.6 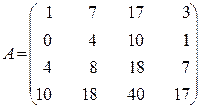
1.7 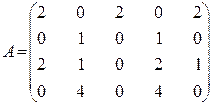 .
.
1.8 
1.9 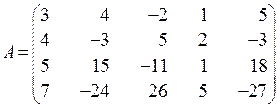
1.10 A= 
1.11 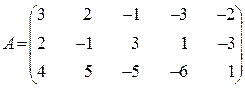 .
.
1.12 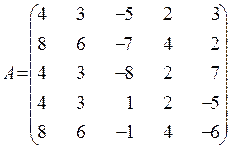
1.13 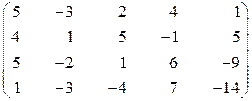
1.14 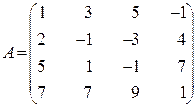
1.15 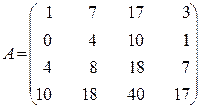
1.16 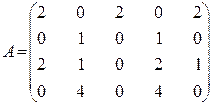 .
.
1.17 
1.18 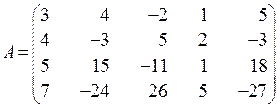
1.19 A= 
1.20 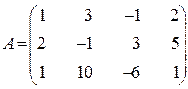 .
.
1.21 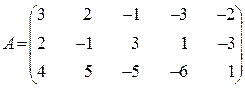 .
.
1.22 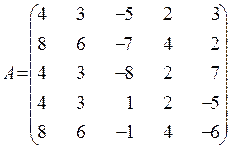
1.23 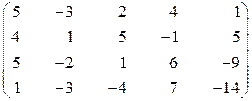
1.24 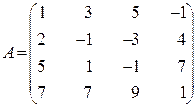
1.25 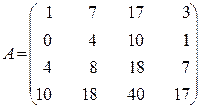
1.26 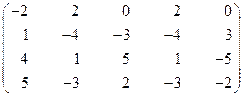
1.27 
1.28 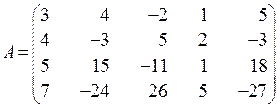
1.29 A= 
1.30 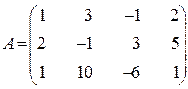 .
.
1.31 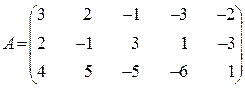 .
.
1.32 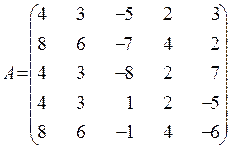
1.33 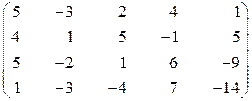
1.34 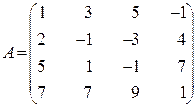
1.35 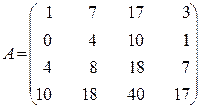
1.36 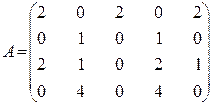 .
.
1.37 
1.38 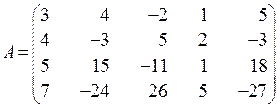
1.39 A= 
1.40 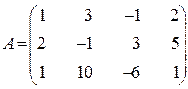 .
.
1.41 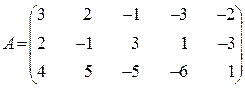 .
.
1.42 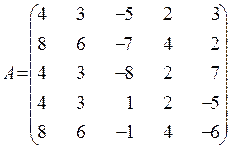
1.43 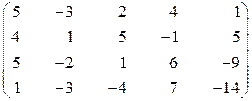
1.44 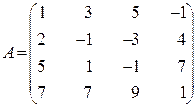
1.45 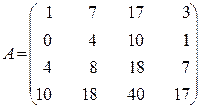
1.46 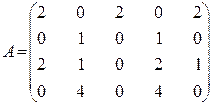 .
.
1.47 
1.48 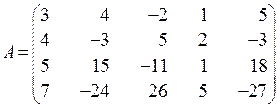
1.49 
1.50 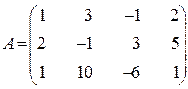 .
.
2 Решить систему уравнений с помощью обратной матрицы:
2.1 
2.2 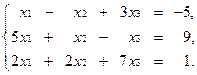
2.3 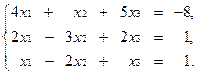
2.4 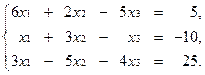
2.5 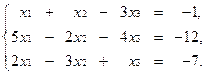
2.6 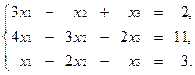
2.7 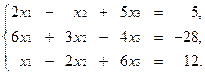
2.8 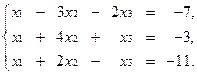
2.9 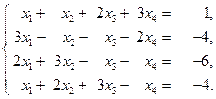
2.10 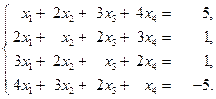
2.11 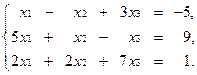
2.12 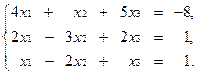
2.13 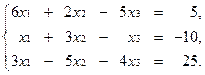
2.14 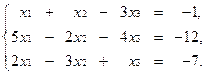
2.15 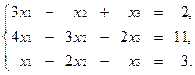
2.16 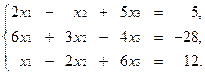
2.17 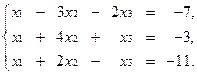
2.18 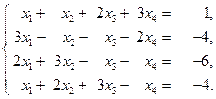
2.19 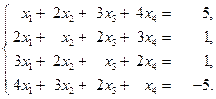
2.20 
2.21 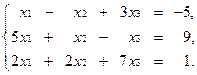
2.22 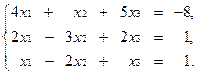
2.23 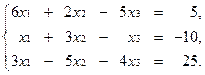
2.24 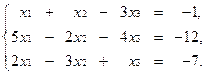
2.25 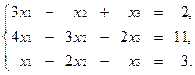
2.26 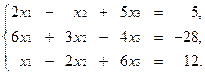
2.27 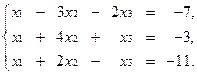
2.28 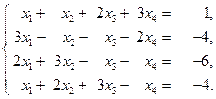
2.29 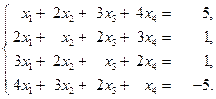
2.30 
2.31 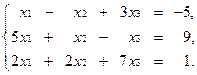
2.32 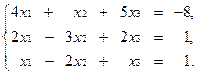
2.33 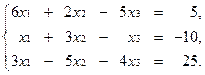
2.34 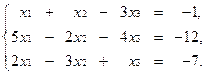
2.35 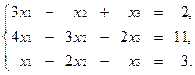
2.36 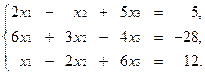
2.37 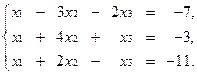
2.38 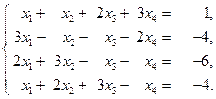
2.39 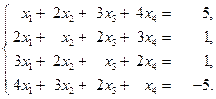
2.40 
2.41 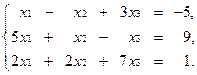
2.42 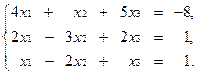
2.43 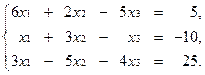
2.44 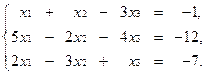
2.45 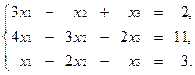
2.46 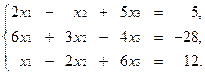
2.47 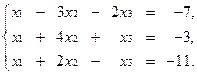
2.48 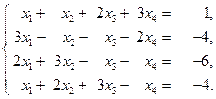
2.49 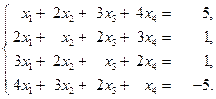
2.50 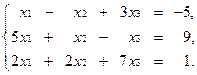
3 Решить геометрическую задачу, при необходимости выполнить чертеж:
3.1Составить канонические уравнения прямой, проведенной через точку 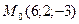 параллельно вектору
параллельно вектору 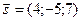 . Лежат ли на этой прямой точки
. Лежат ли на этой прямой точки 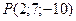 ,
, 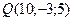 ,
, 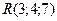 ?
?
3.2 Составить канонические и параметрические уравнения прямой, проходящей через точку 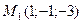 параллельно:
параллельно:
прямой 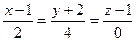 ;
;
3.3 Составить канонические и параметрические уравнения прямой, проходящей через точку 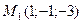 параллельно:
параллельно:
прямой 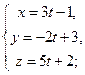
3.4 Дана прямая 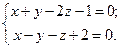 Найти ее канонические уравнения.
Найти ее канонические уравнения.
3.5 Составить канонические уравнения прямой, проходящей через точки  и
и 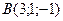 . Представить эту прямую как пересечение двух плоскостей.
. Представить эту прямую как пересечение двух плоскостей.
3.6 Даны вершины треугольника  ,
, 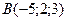 ,
, 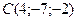 . Составить параметрические уравнения его медианы, проведенной из вершины
. Составить параметрические уравнения его медианы, проведенной из вершины 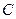 .
.
3.7 Исследовать взаимное расположение двух прямых:
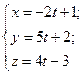 и
и 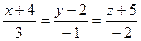
3.8 Исследовать взаимное расположение двух прямых:
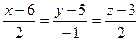 и
и 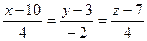 .
.
3.9 Найти угол между двумя прямыми
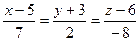 и
и 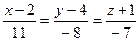 .
.
3.10 Доказать перпендикулярность прямых
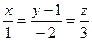 и
и 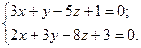
3.11 Составить канонические и параметрические уравнения прямой, проходящей через точку 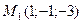 параллельно:
параллельно:
прямой 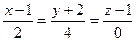 ;
;
3.12 Составить канонические и параметрические уравнения прямой, проходящей через точку 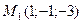 параллельно:
параллельно:
прямой 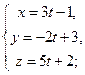
3.13 Дана прямая 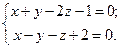 Найти ее канонические уравнения.
Найти ее канонические уравнения.
3.14 Составить канонические уравнения прямой, проходящей через точки  и
и 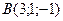 . Представить эту прямую как пересечение двух плоскостей.
. Представить эту прямую как пересечение двух плоскостей.
3.15 Даны вершины треугольника  ,
, 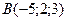 ,
, 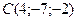 . Составить параметрические уравнения его медианы, проведенной из вершины
. Составить параметрические уравнения его медианы, проведенной из вершины 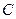 .
.
3.16 Исследовать взаимное расположение двух прямых:
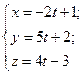 и
и 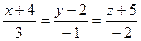
3.17 Исследовать взаимное расположение двух прямых:
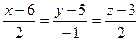 и
и 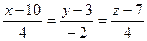 .
.
3.18 Найти угол между двумя прямыми
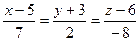 и
и 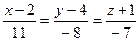 .
.
3.19 Доказать перпендикулярность прямых
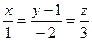 и
и 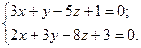
3.20Составить канонические уравнения прямой, проведенной через точку 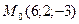 параллельно вектору
параллельно вектору 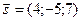 . Лежат ли на этой прямой точки
. Лежат ли на этой прямой точки 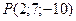 ,
, 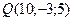 ,
, 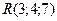 ?
?
3.21 Составить канонические и параметрические уравнения прямой, проходящей через точку 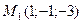 параллельно:
параллельно:
прямой 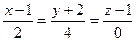 ;
;
3.22 Составить канонические и параметрические уравнения прямой, проходящей через точку 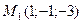 параллельно:
параллельно:
прямой 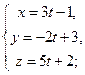
3.23 Дана прямая 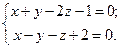 Найти ее канонические уравнения.
Найти ее канонические уравнения.
3.24 Составить канонические уравнения прямой, проходящей через точки  и
и 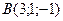 . Представить эту прямую как пересечение двух плоскостей.
. Представить эту прямую как пересечение двух плоскостей.
3.25 Даны вершины треугольника  ,
, 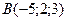 ,
, 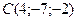 . Составить параметрические уравнения его медианы, проведенной из вершины
. Составить параметрические уравнения его медианы, проведенной из вершины 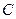 .
.
3.26 Исследовать взаимное расположение двух прямых:
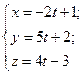 и
и 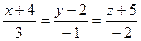
3.27 Исследовать взаимное расположение двух прямых:
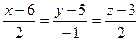 и
и 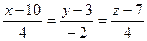 .
.
3.28 Найти угол между двумя прямыми
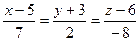 и
и 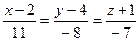 .
.
3.29 Доказать перпендикулярность прямых
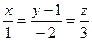 и
и 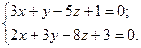
3.30Составить канонические уравнения прямой, проведенной через точку 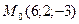 параллельно вектору
параллельно вектору 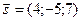 . Лежат ли на этой прямой точки
. Лежат ли на этой прямой точки 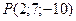 ,
, 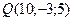 ,
, 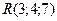 ?
?
3.31 Составить канонические и параметрические уравнения прямой, проходящей через точку 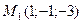 параллельно:
параллельно:
прямой 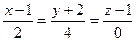 ;
;
3.32 Составить канонические и параметрические уравнения прямой, проходящей через точку 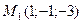 параллельно:
параллельно:
прямой 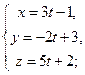
3.33 Дана прямая 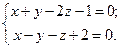 Найти ее канонические уравнения.
Найти ее канонические уравнения.
3.34 Составить канонические уравнения прямой, проходящей через точки  и
и 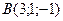 . Представить эту прямую как пересечение двух плоскостей.
. Представить эту прямую как пересечение двух плоскостей.
3.35 Даны вершины треугольника  ,
, 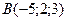 ,
, 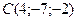 . Составить параметрические уравнения его медианы, проведенной из вершины
. Составить параметрические уравнения его медианы, проведенной из вершины 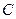 .
.
3.36 Исследовать взаимное расположение двух прямых:
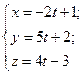 и
и 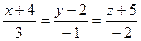
3.37 Исследовать взаимное расположение двух прямых:
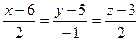 и
и 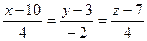 .
.
3.38 Найти угол между двумя прямыми
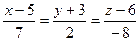 и
и 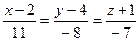 .
.
3.39 Доказать перпендикулярность прямых
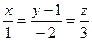 и
и 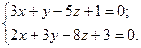
3.40Составить канонические уравнения прямой, проведенной через точку 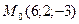 параллельно вектору
параллельно вектору 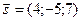 . Лежат ли на этой прямой точки
. Лежат ли на этой прямой точки 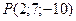 ,
, 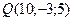 ,
, 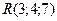 ?
?
3.41 Составить канонические и параметрические уравнения прямой, проходящей через точку 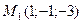 параллельно:
параллельно:
прямой 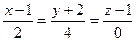 ;
;
3.42 Составить канонические и параметрические уравнения прямой, проходящей через точку 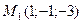 параллельно:
параллельно:
прямой 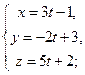
3.43 Дана прямая 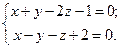 Найти ее канонические уравнения.
Найти ее канонические уравнения.
3.44 Составить канонические уравнения прямой, проходящей через точки  и
и 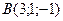 . Представить эту прямую как пересечение двух плоскостей.
. Представить эту прямую как пересечение двух плоскостей.
3.45 Даны вершины треугольника  ,
, 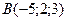 ,
, 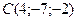 . Составить параметрические уравнения его медианы, проведенной из вершины
. Составить параметрические уравнения его медианы, проведенной из вершины 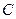 .
.
3.46 Исследовать взаимное расположение двух прямых:
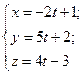 и
и 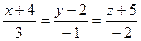
3.47 Исследовать взаимное расположение двух прямых:
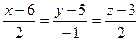 и
и 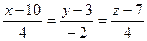 .
.
3.48 Найти угол между двумя прямыми
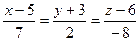 и
и 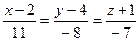 .
.
3.49 Доказать перпендикулярность прямых
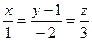 и
и 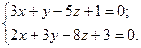
3.50 Составить канонические и параметрические уравнения прямой, проходящей через точку 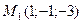 параллельно:
параллельно:
прямой 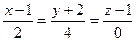 ;
;
4 Решить задачу по векторной алгебре при необходимости выполнить чертеж:
4.1 Даны точки 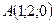 ,
, 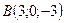 ,
, 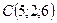 . Вычислить площадь треугольника
. Вычислить площадь треугольника 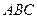 .
.
4.2 Сила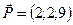 приложена к точке
приложена к точке 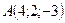 . Определить величину и направляющие косинусы момента этой силы относительно точки
. Определить величину и направляющие косинусы момента этой силы относительно точки 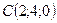 .
.
4.3 Вектор 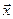 , перпендикулярный к векторам
, перпендикулярный к векторам 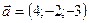 и
и 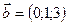 , образует с осью
, образует с осью 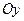 тупой угол. Зная, что
тупой угол. Зная, что 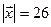 , найти его координаты.
, найти его координаты.
4.4 Найти площадь параллелограмма, диагоналями которого служат векторы 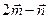 и
и 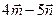 , где
, где  и
и 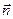 - единичные векторы, образующие угол
- единичные векторы, образующие угол 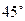 .
.
4.5 Найти смешанное произведение трех векторов 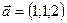 ,
,  ,
, 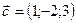 . Определить правую или левую тройку образуют векторы
. Определить правую или левую тройку образуют векторы 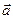 ,
, 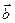 ,
, 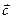 ?
?
4.6 Доказать, что векторы 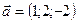 ,
, 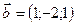 ,
, 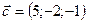 компланарны.
компланарны.
4.7 Доказать, что точки 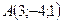 ,
, 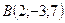 ,
, 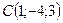 ,
, 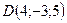 лежат в одной плоскости.
лежат в одной плоскости.
4.8 Векторы 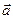 ,
, 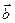 ,
, 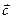 удовлетворяют условию
удовлетворяют условию 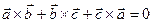 . Доказать, что эти векторы компланарны.
. Доказать, что эти векторы компланарны.
4.9 Найти объем тетраэдра, построенного на векторах 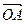 ,
, 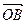 и
и 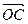 , если эти векторы направлены по биссектрисам координатных полуплоскостей, и длина каждого вектора равна 2.
, если эти векторы направлены по биссектрисам координатных полуплоскостей, и длина каждого вектора равна 2.
4.10 Даны вершины тетраэдра: 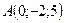 ,
, 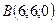 ,
, 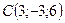 ,
, 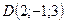 . Найти его объем и длину высоты, опущенной из вершины
. Найти его объем и длину высоты, опущенной из вершины 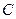 .
.
4.11 Доказать, что 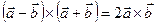 , и выяснить геометрическое значение этого тождества.
, и выяснить геометрическое значение этого тождества.
4.12 Даны векторы 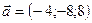 ,
, 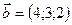 . Найти их векторное произведение, синус угла между ними, площадь параллелограмма построенного на этих векторах.
. Найти их векторное произведение, синус угла между ними, площадь параллелограмма построенного на этих векторах.
4.13 Доказать, что точки 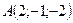 ,
, 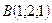 ,
,  и
и 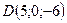 лежат в одной плоскости.
лежат в одной плоскости.
4.14 Дан треугольник с вершинами 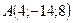 ,
, 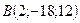 ,
, 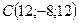 . Найти длину его высоты, опущенной из вершины
. Найти длину его высоты, опущенной из вершины 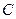 на сторону
на сторону 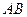 .
.
4.15 Найти объем параллелепипеда, построенного на векторах 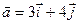 ,
, 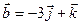 ,
,  и определить, правой или левой является тройка векторов
и определить, правой или левой является тройка векторов 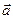 ,
, 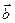 ,
, 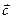 .
.
4.16 Даны две силы 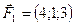 ,
, 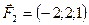 , приложенные в точке
, приложенные в точке 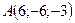 . Определить величину и направляющие косинусы момента равнодействующей этих сил относительно точки
. Определить величину и направляющие косинусы момента равнодействующей этих сил относительно точки 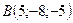 .
.
4.17 Доказать, что векторы 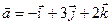 ,
, 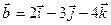 ,
, 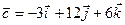 компланарны.
компланарны.
4.18 Векторы 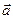 и
и 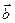 составляют угол
составляют угол 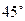 . Найти площадь треугольника, построенного на векторах
. Найти площадь треугольника, построенного на векторах 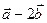 и
и 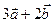 , если
, если 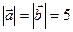 .
.
4.19 Найти объем пирамиды с вершинами в точках: 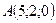 ,
, 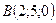 ,
, 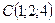 и
и 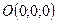 .
.
4.20 Найти площадь параллелограмма, построенного на векторах 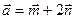 и
и 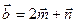 , где
, где  и
и 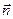 - единичные векторы, образующие угол
- единичные векторы, образующие угол 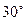 .
.
4.21 Найти смешанное произведение трех векторов: 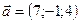 ,
, 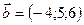 ,
, 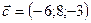 . Какую тройку векторов они образуют?
. Какую тройку векторов они образуют?
4.22 Сила 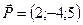 приложена к точке
приложена к точке 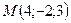 . Определить момент этой силы относительно точки
. Определить момент этой силы относительно точки 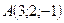 .
.
4.23 Доказать тождество 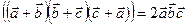 .
.
4.24 Сила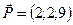 приложена к точке
приложена к точке 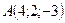 . Определить величину и направляющие косинусы момента этой силы относительно точки
. Определить величину и направляющие косинусы момента этой силы относительно точки 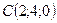 .
.
4.25 Вектор 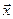 , перпендикулярный к векторам
, перпендикулярный к векторам 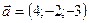 и
и 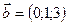 , образует с осью
, образует с осью 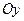 тупой угол. Зная, что
тупой угол. Зная, что 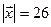 , найти его координаты.
, найти его координаты.
4.26 Найти площадь параллелограмма, диагоналями которого служат векторы 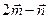 и
и 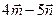 , где
, где  и
и 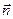 - единичные векторы, образующие угол
- единичные векторы, образующие угол 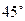 .
.
4.27 Найти смешанное произведение трех векторов 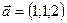 ,
,  ,
, 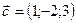 . Определить правую или левую тройку образуют векторы
. Определить правую или левую тройку образуют векторы 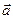 ,
, 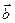 ,
, 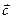 ?
?
4.28 Доказать, что векторы 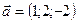 ,
, 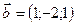 ,
, 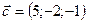 компланарны.
компланарны.
4.29 Доказать, что точки 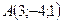 ,
, 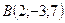 ,
, 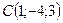 ,
, 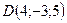 лежат в одной плоскости.
лежат в одной плоскости.
4.30 Векторы 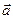 ,
, 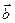 ,
, 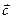 удовлетворяют условию
удовлетворяют условию 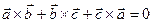 . Доказать, что эти векторы компланарны.
. Доказать, что эти векторы компланарны.
4.31 Найти объем тетраэдра, построенного на векторах 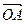 ,
, 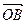 и
и 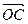 , если эти векторы направлены по биссектрисам координатных полуплоскостей, и длина каждого вектора равна 2.
, если эти векторы направлены по биссектрисам координатных полуплоскостей, и длина каждого вектора равна 2.
4.32 Даны вершины тетраэдра: 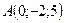 ,
, 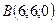 ,
, 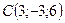 ,
, 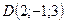 . Найти его объем и длину высоты, опущенной из вершины
. Найти его объем и длину высоты, опущенной из вершины 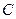 .
.
4.33 Доказать, что 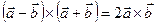 , и выяснить геометрическое значение этого тождества.
, и выяснить геометрическое значение этого тождества.
4.34 Даны векторы 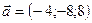 ,
, 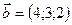 . Найти их векторное произведение, синус угла между ними, площадь параллелограмма построенного на этих векторах.
. Найти их векторное произведение, синус угла между ними, площадь параллелограмма построенного на этих векторах.
4.35 Доказать, что точки 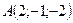 ,
, 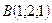 ,
,  и
и 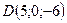 лежат в одной плоскости.
лежат в одной плоскости.
4.36 Дан треугольник с вершинами 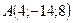 ,
, 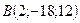 ,
, 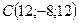 . Найти длину его высоты, опущенной из вершины
. Найти длину его высоты, опущенной из вершины 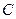 на сторону
на сторону 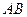 .
.
4.37 Найти объем параллелепипеда, построенного на векторах 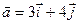 ,
, 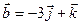 ,
,  и определить, правой или левой является тройка векторов
и определить, правой или левой является тройка векторов 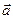 ,
, 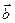 ,
, 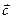 .
.
4.38 Даны две силы 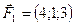 ,
, 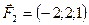 , приложенные в точке
, приложенные в точке 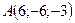 . Определить величину и направляющие косинусы момента равнодействующей этих сил относительно точки
. Определить величину и направляющие косинусы момента равнодействующей этих сил относительно точки 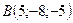 .
.
4.39 Доказать, что векторы 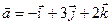 ,
, 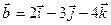 ,
, 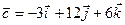 компланарны.
компланарны.
4.1 Даны точки 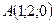 ,
, 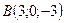 ,
, 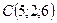 . Вычислить площадь треугольника
. Вычислить площадь треугольника 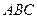 .
.
4.40 Сила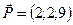 приложена к точке
приложена к точке 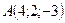 . Определить величину и направляющие косинусы момента этой силы относительно точки
. Определить величину и направляющие косинусы момента этой силы относительно точки 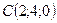 .
.
4.41 Вектор 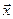 , перпендикулярный к векторам
, перпендикулярный к векторам 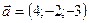 и
и 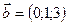 , образует с осью
, образует с осью 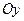 тупой угол. Зная, что
тупой угол. Зная, что 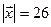 , найти его координаты.
, найти его координаты.
4.42 Найти площадь параллелограмма, диагоналями которого служат векторы 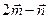 и
и 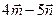 , где
, где  и
и 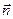 - единичные векторы, образующие угол
- единичные векторы, образующие угол 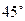 .
.
4.43 Найти смешанное произведение трех векторов 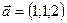 ,
,  ,
, 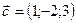 . Определить правую или левую тройку образуют векторы
. Определить правую или левую тройку образуют векторы 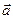 ,
, 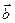 ,
, 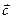 ?
?
4.44 Доказать, что векторы 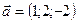 ,
, 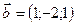 ,
, 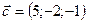 компланарны.
компланарны.
4.45 Доказать, что точки 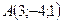 ,
, 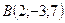 ,
, 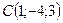 ,
, 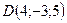 лежат в одной плоскости.
лежат в одной плоскости.
4.46 Векторы 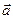 ,
, 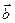 ,
, 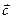 удовлетворяют условию
удовлетворяют условию 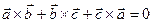 . Доказать, что эти векторы компланарны.
. Доказать, что эти векторы компланарны.
4.47 Найти объем тетраэдра, построенного на векторах 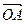 ,
, 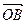 и
и 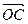 , если эти векторы направлены по биссектрисам координатных полуплоскостей, и длина каждого вектора равна 2.
, если эти векторы направлены по биссектрисам координатных полуплоскостей, и длина каждого вектора равна 2.
4.48 Даны вершины тетраэдра: 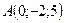 ,
, 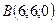 ,
, 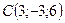 ,
, 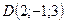 . Найти его объем и длину высоты, опущенной из вершины
. Найти его объем и длину высоты, опущенной из вершины 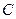 .
.
4.49 Доказать, что 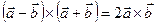 , и выяснить геометрическое значение этого тождества.
, и выяснить геометрическое значение этого тождества.
4.50 Найти объем параллелепипеда, построенного на векторах 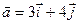 ,
, 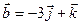 ,
,  и определить, правой или левой является тройка векторов
и определить, правой или левой является тройка векторов 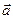 ,
, 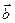 ,
, 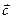 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|