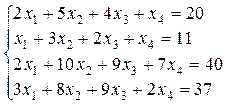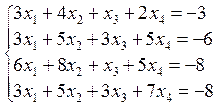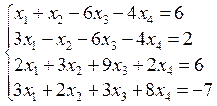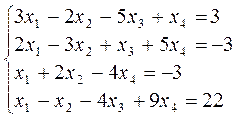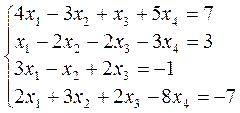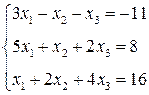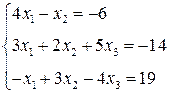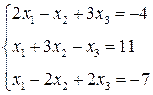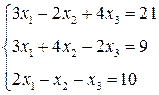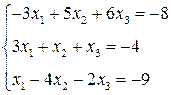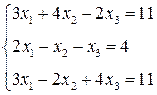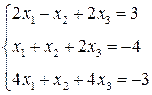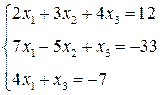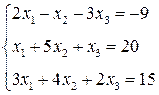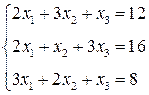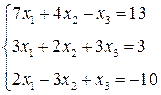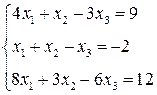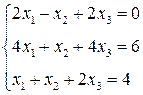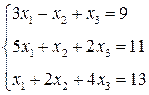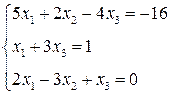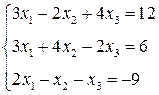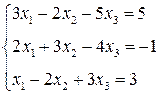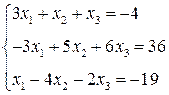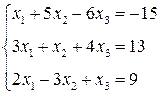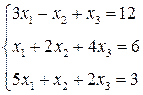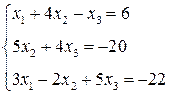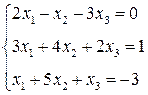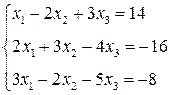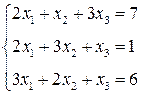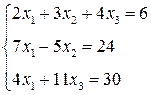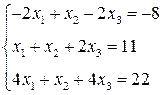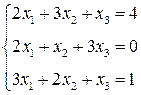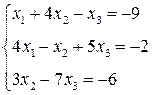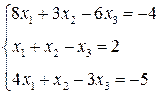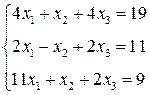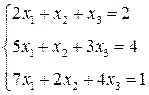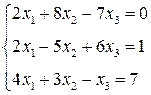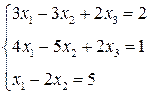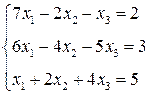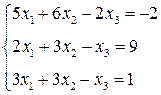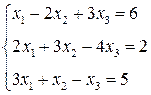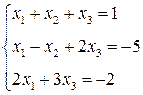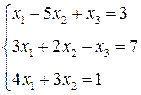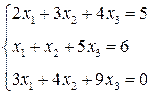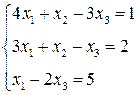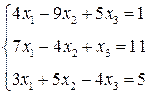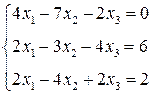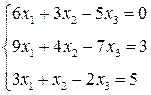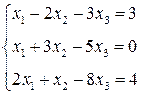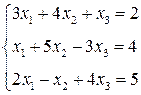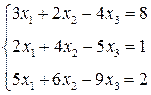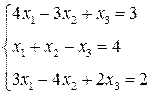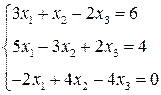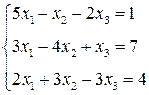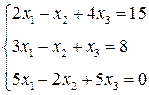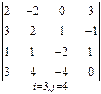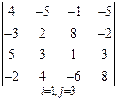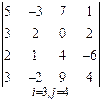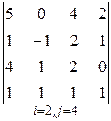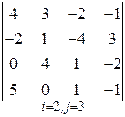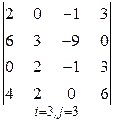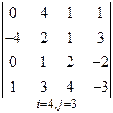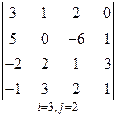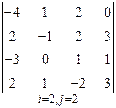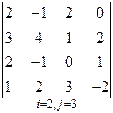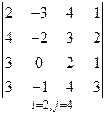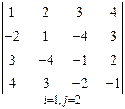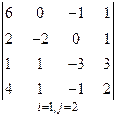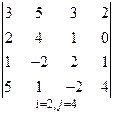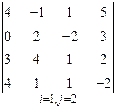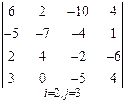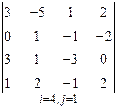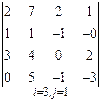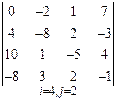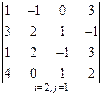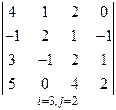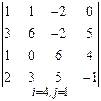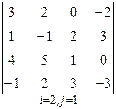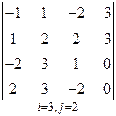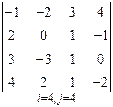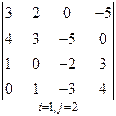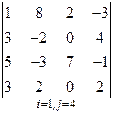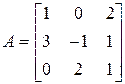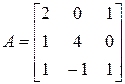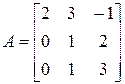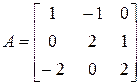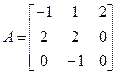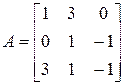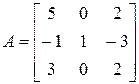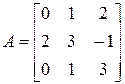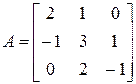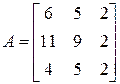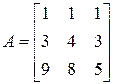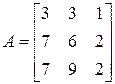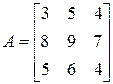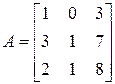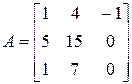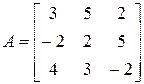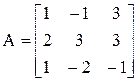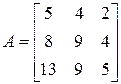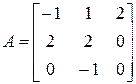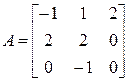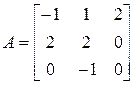- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ЛІНІЙНА АЛГЕБРА. Розв’язати однорідну систему лінійних алгебраїчних рівнянь одним із відомих вам методів
Тема:
ЛІНІЙНА АЛГЕБРА
( матриці, визначники, системи лінійних рівнянь)
1. Відповідно до свого варіанта виконайте обчислення значень функцій f1(x) і f2(x) та побудуйте в одній системі координат їх графіки:. для аналітично заданої функції 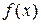 скласти на проміжку
скласти на проміжку 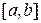 таблицю зі значеннями х в точках (значення
таблицю зі значеннями х в точках (значення 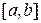 підбирає студент на свій розсуд).
підбирає студент на свій розсуд).
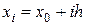 ,
, 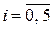 ,
, 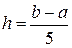 ,
, 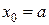 ,
, 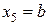 .
.
| № |
| |
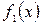 =x4-8x2+8x+5 =x4-8x2+8x+5
|  =x4+4x2-44x+3 =x4+4x2-44x+3
| |
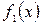 =-x4+8x2-8x+3 =-x4+8x2-8x+3
|  =x4-4x2-20x+2 =x4-4x2-20x+2
| |
 =x4-8x2+8x+1 =x4-8x2+8x+1
|  =2x5+20x2-20x+3 =2x5+20x2-20x+3
| |
 =x4-4x3-12x+1 =x4-4x3-12x+1
|  =2x5+20x2-20x+10 =2x5+20x2-20x+10
| |
 =x4+8x2-12x+5 =x4+8x2-12x+5
|  =x6-18x2+12x+3 =x6-18x2+12x+3
| |
 =x5+10x2-10x+3 =x5+10x2-10x+3
|  =x6-18x2+12x+1 =x6-18x2+12x+1
| |
 =x5+10x2-10x+2 =x5+10x2-10x+2
|  =0.1x6-1.8x2+1.2x+0.3 =0.1x6-1.8x2+1.2x+0.3
| |
 =x3-0.3x2-2.97x =x3-0.3x2-2.97x
|  =3x4-16x3+24x =3x4-16x3+24x
| |
 =-x3+0.3x2-2.97x-1 =-x3+0.3x2-2.97x-1
|  =0.3x4-1.6x3+2.4x =0.3x4-1.6x3+2.4x
| |
 =3x4+20x3-90x-84 =3x4+20x3-90x-84
|  =3x4-16x3+24x+10 =3x4-16x3+24x+10
| |
 =3x4-0.8x3-1.2x2-14.4x =3x4-0.8x3-1.2x2-14.4x
|  =3x4-12x2-60x+2 =3x4-12x2-60x+2
| |
 =0.25x4-4/3x3+5x2-10x =0.25x4-4/3x3+5x2-10x
|  =x6-12x+18 =x6-12x+18
| |
 =x4+2x2-4x+3 =x4+2x2-4x+3
|  =x4-4x2-20x+3 =x4-4x2-20x+3
| |
 =x4-2x2-4x+5 =x4-2x2-4x+5
|  =-1.2x3+12.3x2-9.3x-197 =-1.2x3+12.3x2-9.3x-197
| |
 =x6-12x+18 =x6-12x+18
|  =1.3x3+6.4x2-1.5x-27 =1.3x3+6.4x2-1.5x-27
| |
 =x4-8x2+8x+5 =x4-8x2+8x+5
|  =x4+4x2-44x+3 =x4+4x2-44x+3
| |
 =-x4+8x2-8x+3 =-x4+8x2-8x+3
|  =x4-4x2-20x+2 =x4-4x2-20x+2
| |
 =x4-8x2+8x+1 =x4-8x2+8x+1
|  =2x5+20x2-20x+3 =2x5+20x2-20x+3
| |
 =x4-4x3-12x+1 =x4-4x3-12x+1
|  =2x5+20x2-20x+10 =2x5+20x2-20x+10
| |
 =x4+8x2-12x+5 =x4+8x2-12x+5
|  =x6-18x2+12x+3 =x6-18x2+12x+3
| |
 =x5+10x2-10x+3 =x5+10x2-10x+3
|  =x6-18x2+12x+1 =x6-18x2+12x+1
| |
 =x5+10x2-10x+2 =x5+10x2-10x+2
|  =0.1x6-1.8x2+1.2x+0.3 =0.1x6-1.8x2+1.2x+0.3
| |
 =x3-0.3x2-2.97x =x3-0.3x2-2.97x
|  =3x4-16x3+24x =3x4-16x3+24x
| |
 =-x3+0.3x2-2.97x-1 =-x3+0.3x2-2.97x-1
|  =0.3x4-1.6x3+2.4x =0.3x4-1.6x3+2.4x
| |
 =3x4+20x3-90x-84 =3x4+20x3-90x-84
|  =3x4-16x3+24x+10 =3x4-16x3+24x+10
| |
 =3x4-0.8x3-1.2x2-14.4x =3x4-0.8x3-1.2x2-14.4x
|  =3x4-12x2-60x+2 =3x4-12x2-60x+2
| |
 =0.25x4-4/3x3+5x2-10x =0.25x4-4/3x3+5x2-10x
|  =x6-12x+18 =x6-12x+18
| |
 =x4+2x2-4x+3 =x4+2x2-4x+3
|  =x4-4x2-20x+3 =x4-4x2-20x+3
| |
 =x4-2x2-4x+5 =x4-2x2-4x+5
|  =-1.2x3+12.3x2-9.3x-197 =-1.2x3+12.3x2-9.3x-197
| |
 =x6-12x+18 =x6-12x+18
|  =1.3x3+6.4x2-1.5x-27 =1.3x3+6.4x2-1.5x-27
| |
 =x5+10x2-10x+3 =x5+10x2-10x+3
|  =0.1x6-1.8x2+1.2x+0.3 =0.1x6-1.8x2+1.2x+0.3
| |
 =-x4+8x2-8x+3 =-x4+8x2-8x+3
|  =2x5+20x2-20x+10 =2x5+20x2-20x+10
| |
 =x4+8x2-12x+5 =x4+8x2-12x+5
|  =2x5+20x2-20x+10 =2x5+20x2-20x+10
| |
 =x5+10x2-10x+3 =x5+10x2-10x+3
|  =x4+4x2-44x+3 =x4+4x2-44x+3
| |
 =x5+10x2-10x+3 =x5+10x2-10x+3
|  =x6-18x2+12x+3 =x6-18x2+12x+3
| |
 =x5+10x2-10x+2 =x5+10x2-10x+2
|  =x6-18x2+12x+1 =x6-18x2+12x+1
| |
 =x3-0.3x2-2.97x =x3-0.3x2-2.97x
|  =0.1x6-1.8x2+1.2x+0.3 =0.1x6-1.8x2+1.2x+0.3
| |
 =-x3+0.3x2-2.97x-1 =-x3+0.3x2-2.97x-1
|  =3x4-16x3+24x =3x4-16x3+24x
| |
 =3x4+20x3-90x-84 =3x4+20x3-90x-84
|  =0.3x4-1.6x3+2.4x =0.3x4-1.6x3+2.4x
| |
 =3x4-0.8x3-1.2x2-14.4x =3x4-0.8x3-1.2x2-14.4x
|  =3x4-16x3+24x+10 =3x4-16x3+24x+10
| |
 =0.25x4-4/3x3+5x2-10x =0.25x4-4/3x3+5x2-10x
|  =3x4-12x2-60x+2 =3x4-12x2-60x+2
| |
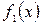 =-x4+8x2-8x+3 =-x4+8x2-8x+3
|  =3x4-16x3+24x+10 =3x4-16x3+24x+10
| |
 =x4-8x2+8x+1 =x4-8x2+8x+1
|  =3x4-12x2-60x+2 =3x4-12x2-60x+2
| |
 =x4-4x3-12x+1 =x4-4x3-12x+1
|  =x6-12x+18 =x6-12x+18
| |
 =x4+8x2-12x+5 =x4+8x2-12x+5
|  =x4-4x2-20x+3 =x4-4x2-20x+3
| |
 =x5+10x2-10x+3 =x5+10x2-10x+3
|  =-1.2x3+12.3x2-9.3x-197 =-1.2x3+12.3x2-9.3x-197
| |
 =x5+10x2-10x+2 =x5+10x2-10x+2
|  =1.3x3+6.4x2-1.5x-27 =1.3x3+6.4x2-1.5x-27
| |
 =x3-0.3x2-2.97x =x3-0.3x2-2.97x
|  =x4+4x2-44x+3 =x4+4x2-44x+3
| |
 =-x3+0.3x2-2.97x-1 =-x3+0.3x2-2.97x-1
|  =x4-4x2-20x+2 =x4-4x2-20x+2
| |
 =x4-8x2+8x+1 =x4-8x2+8x+1
|  =2x5+20x2-20x+3 =2x5+20x2-20x+3
| |
2. Проведіть обчислення та побудуйте графік функції Z = f (x,y), згідно зі своїм варіантом (значення x,y студент підбирає на свій розсуд).
| № | Завдання | № | Завдання | № | Завдання |
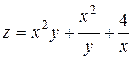
| 
| 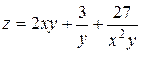
| |||
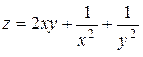
| 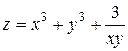
| 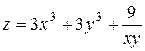
| |||
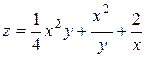
| 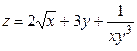
| 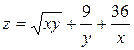
| |||
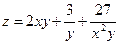
| 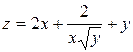
| 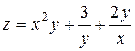
| |||
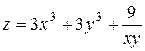
| 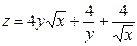
| 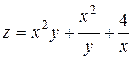
| |||
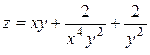
| 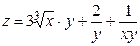
| 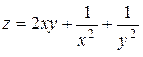
| |||
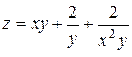
| 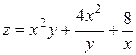
| 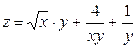
| |||
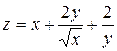
| 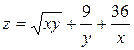
| 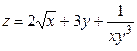
| |||
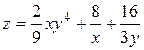
| 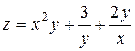
| 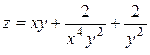
| |||
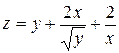
| 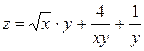
| 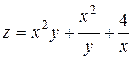
| |||
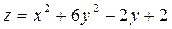
| 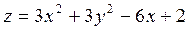
| 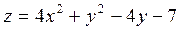
| |||
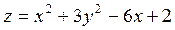
| 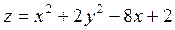
| 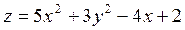
| |||
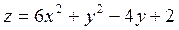
| 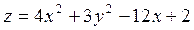
| 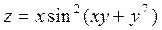
| |||
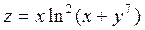
| 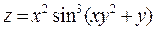
| 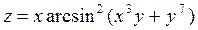
| |||
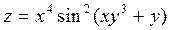
| 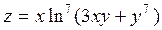
| 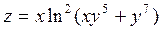
| |||
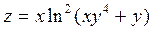
| 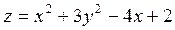
| 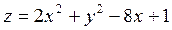
| |||
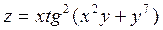
| 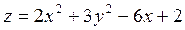
|
3. Розв’язати однорідну систему лінійних алгебраїчних рівнянь одним із відомих вам методів
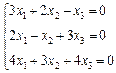
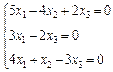
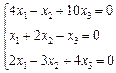
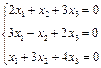
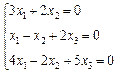
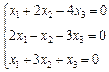
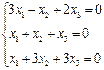
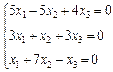
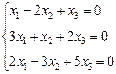
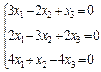
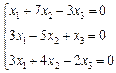
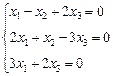
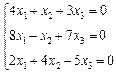
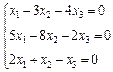
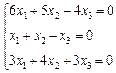
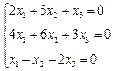
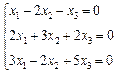
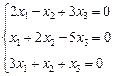
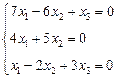
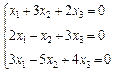
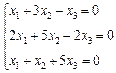
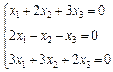
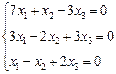
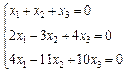
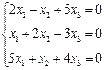
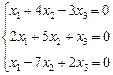
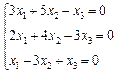

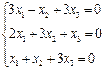
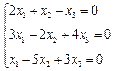
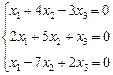
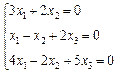
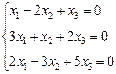
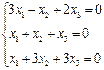
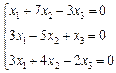
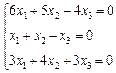
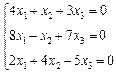
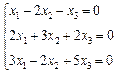
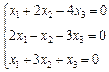
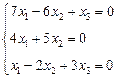
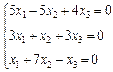
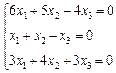
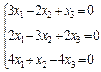
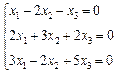
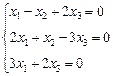
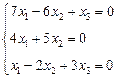
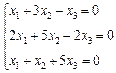
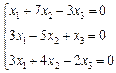
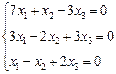
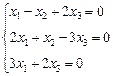
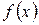
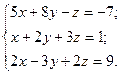 2.
2. 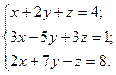 3.
3. 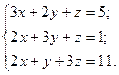 4.
4. 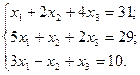 5.
5. 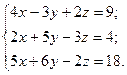 6.
6. 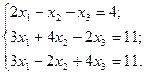 7.
7. 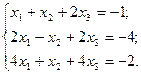 8.
8. 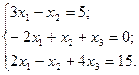 9.
9. 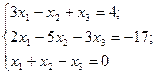 10.
10. 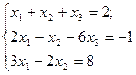 11.
11. 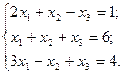 12.
12. 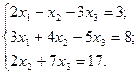 13.
13. 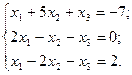 14.
14. 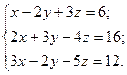 15.
15. 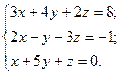
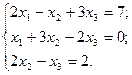 27
27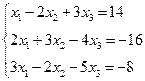 28
28 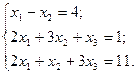 29
29 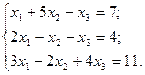 30
30 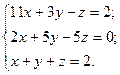 31
31 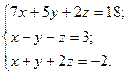 32
32  33
33 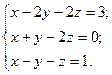 34
34 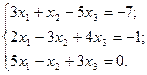 35
35 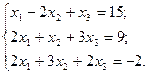 36
36 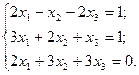 37
37 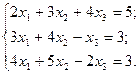 38
38 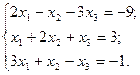 39
39 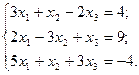 40
40 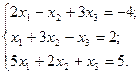
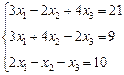
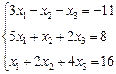

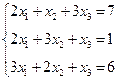
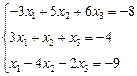
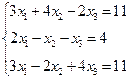
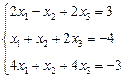
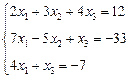
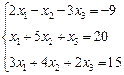
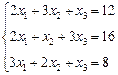
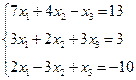
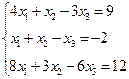
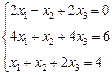
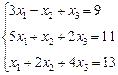
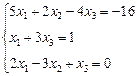
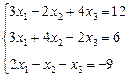
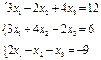
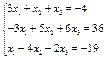
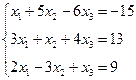
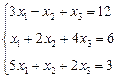
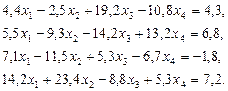
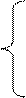
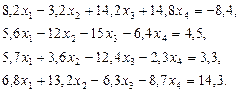
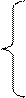
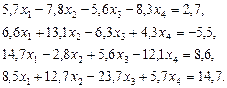
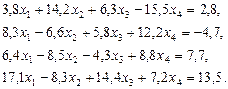
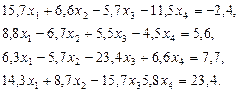
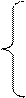
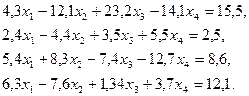
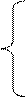
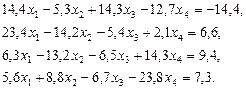
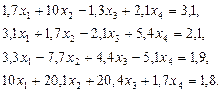
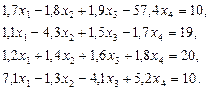
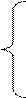
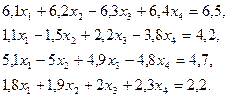
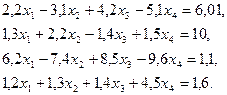
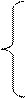
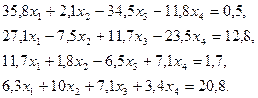
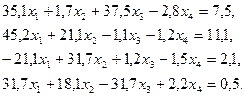
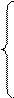
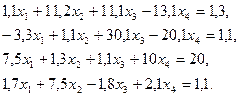
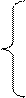
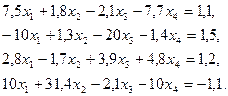
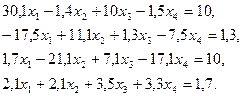
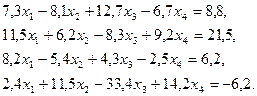
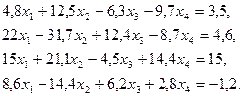
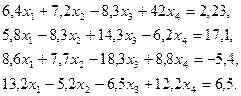
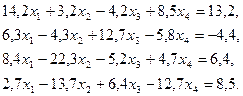
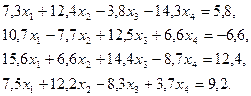
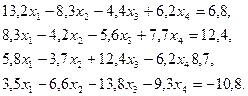
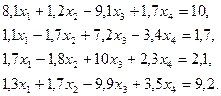
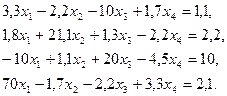
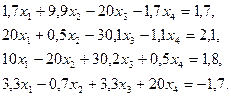
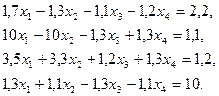
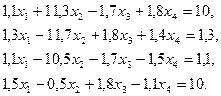
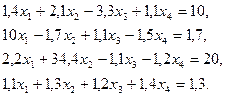
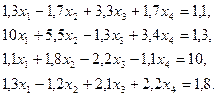
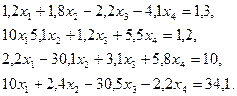
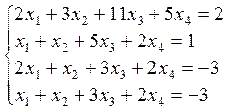 ;
;