- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Методы интегрирования заменой переменной и по частям.
Тема: Методы интегрирования заменой переменной и по частям.
Теоретические сведения к практической работе
Функция 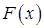 , определенная на интервале
, определенная на интервале 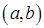 , называется первообразной для функции
, называется первообразной для функции 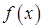 , определенной на том же интервале
, определенной на том же интервале 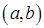 , если
, если 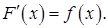
Если 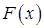 — первообразная для функции
— первообразная для функции 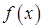 , то любая другая первообразная
, то любая другая первообразная 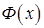 для функции
для функции 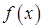 отличается от
отличается от 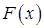 на некоторое постоянное слагаемое, т. е.
на некоторое постоянное слагаемое, т. е. 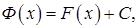 где
где 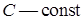 .
.
Неопределенным интегралом от функции 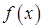 называется совокупность всех первообразных для этой функции. Обозначается неопределенный интеграл:
называется совокупность всех первообразных для этой функции. Обозначается неопределенный интеграл: 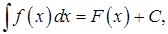 где
где 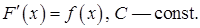
Операция нахождений первообразной для данной функции называется интегрированием. Интегрирование является обратной операцией к дифференцированию:
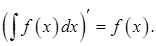
Для проверки правильности выполненного интегрирования необходимо продифференцировать результат интегрирования и сравнить полученную функцию с подынтегральной.
Свойства неопределенного интеграла:
1. 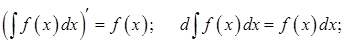
2. 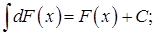
3. 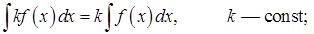
4. 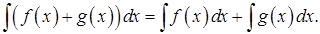
Таблица основных интегралов
1. 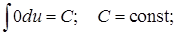 2.
2. 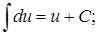
3. 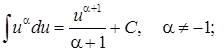
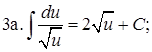
4. 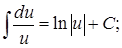 5.
5. 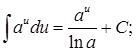
6. 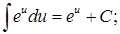 7.
7. 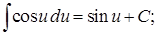
8. 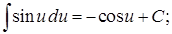 9.
9. 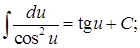
10. 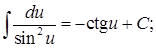 11.
11. 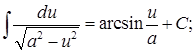
12. 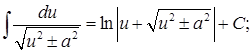 13.
13. 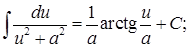
14. 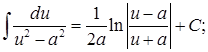 15.
15. 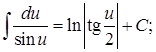
16. 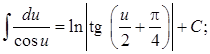 17.
17. 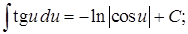
18. 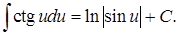
Каждая из приведенных в таблице формул справедлива на промежутке, не содержащем точек разрыва подынтегральной функции. Вычисление интегралов с использованием таблицы и основных свойств называют непосредственным интегрированием.
Пример 1. Пользуясь таблицей основных интегралов и свойствами неопределенного интеграла, найти интегралы (результат интегрирования проверить дифференцированием):
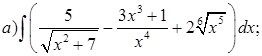
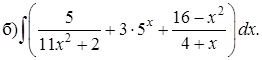
Решение.
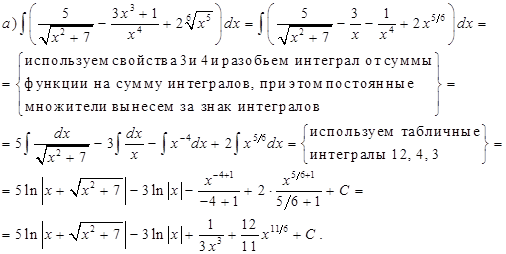 Проверка:
Проверка:
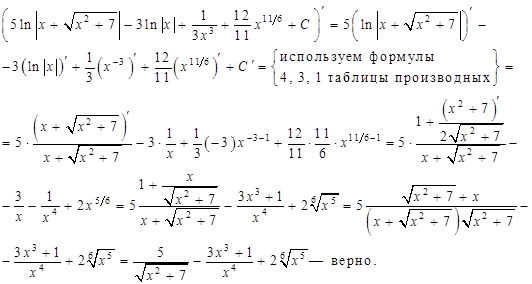
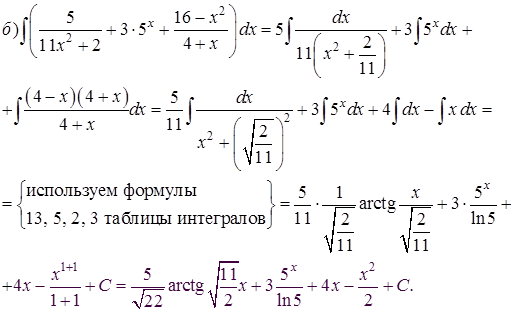
Проверка:
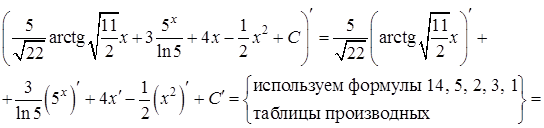
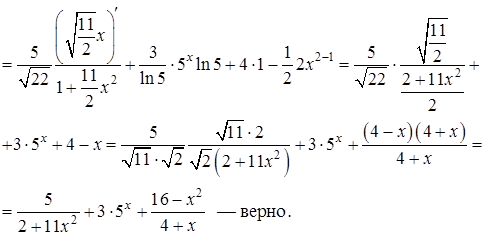
Метод замены переменной
Теорема 1. Пусть 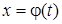 монотонная, непрерывно дифференцируемая функция, тогда
монотонная, непрерывно дифференцируемая функция, тогда
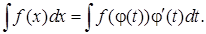 (1)
(1)
При этом, если 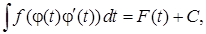 то
то 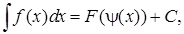 где
где 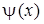 — функция, обратная
— функция, обратная 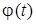 .
.
Формула (1) называется формулой замены переменной в неопределенном интеграле.
Алгоритм замены переменной:
1) Связать старую переменную интегрирования 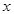 с новой переменной
с новой переменной 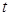 с помощью замены
с помощью замены 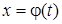 .
.
2) Найти связь между дифференциалами 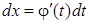 .
.
3) Перейти под знаком интеграла к новой переменной.
4) Проинтегрировать и в полученной первообразной вернуться к старой переменной, подставив 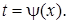
Пример 2. Проинтегрировать подходящей заменой переменной.
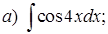
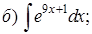
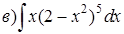
Решение:
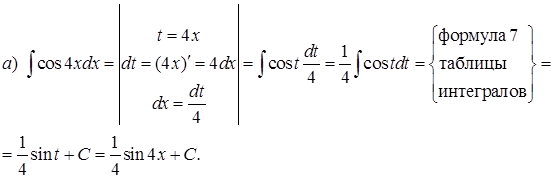
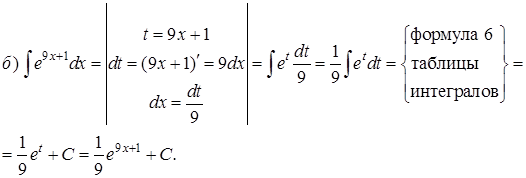
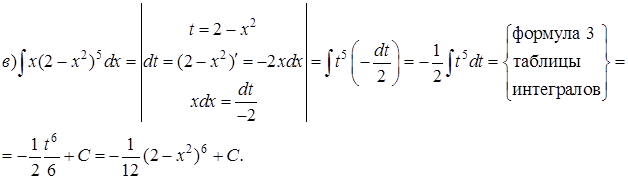
Интегрирование по частям.
Некоторые виды интегралов, вычисляемых по частям
Если производные функций 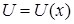 и
и 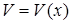 непрерывны, то справедлива формула:
непрерывны, то справедлива формула:

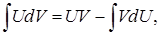 (3)
(3)
называемая формулой интегрирования по частям.
В качестве 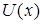 обычно выбирают функцию, которая упрощается при дифференцировании.
обычно выбирают функцию, которая упрощается при дифференцировании.
Некоторые стандартные случаи функций, интегрируемых по частям, указаны в таблице 1. Там же дается способ выбора множителей 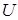 и
и 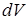 .
.
Таблица 1
| Вид интеграла | 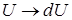
| 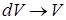
|
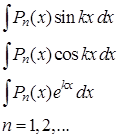
| 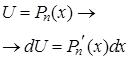
| 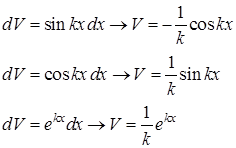
|
| Вид интеграла | 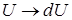
| 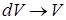
|
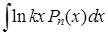
| 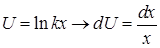
|
|
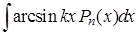
| 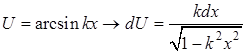
| |
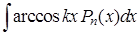
| 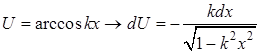
| |
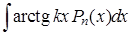
| 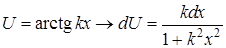
| |
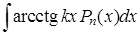
| 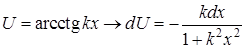
| |
|
| ||
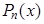 — многочлен от
— многочлен от 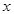 степени
степени 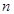 , т. е.
, т. е. 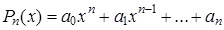 , где
, где 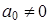 .
.
Пример 3.Проинтегрировать по частям.
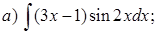
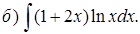
Решение.
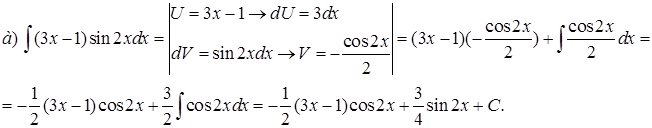
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|