Конечные матричные игры

2. Конечные матричные игры

2.1) Игра 2*xm

1. Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях.
Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.

Игроки	B₁	B₂	B₃	B₄	B₅	B₆	B₇	B₈	B₉	a = min(A_i)
A₁	-10	-6					-15	-12		-15
A₂	-16	-2		-10				-14	-5	-16
b = max(B_i)	-10	-2						-12

Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(a_i) = -15, которая указывает на максимальную чистую стратегию A₁.
Верхняя цена игры b = min(b_j) = -12.
Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах -15 ≤ y ≤ -12. Находим решение игры в смешанных стратегиях. Объясняется это тем, что игроки не могут объявить противнику свои чистые стратегии: им следует скрывать свои действия. Игру можно решить, если позволить игрокам выбирать свои стратегии случайным образом (смешивать чистые стратегии).
2. Проверяем платежную матрицу на доминирующие строки и доминирующие столбцы.
С позиции проигрышей игрока В стратегия B₁ доминирует над стратегией B₂ (все элементы столбца 1 меньше элементов столбца 2), следовательно, исключаем 2-й столбец матрицы. Вероятность q₂ = 0.
С позиции проигрышей игрока В стратегия B₁ доминирует над стратегией B₃ (все элементы столбца 1 меньше элементов столбца 3), следовательно, исключаем 3-й столбец матрицы. Вероятность q₃ = 0.
С позиции проигрышей игрока В стратегия B₁ доминирует над стратегией B₄ (все элементы столбца 1 меньше элементов столбца 4), следовательно, исключаем 4-й столбец матрицы. Вероятность q₄ = 0.
С позиции проигрышей игрока В стратегия B₁ доминирует над стратегией B₅ (все элементы столбца 1 меньше элементов столбца 5), следовательно, исключаем 5-й столбец матрицы. Вероятность q₅ = 0.
С позиции проигрышей игрока В стратегия B₁ доминирует над стратегией B₆ (все элементы столбца 1 меньше элементов столбца 6), следовательно, исключаем 6-й столбец матрицы. Вероятность q₆ = 0.
С позиции проигрышей игрока В стратегия B₁ доминирует над стратегией B₉ (все элементы столбца 1 меньше элементов столбца 9), следовательно, исключаем 9-й столбец матрицы. Вероятность q₉ = 0.

-10	-15	-12
-16		-14

В платежной матрице отсутствуют доминирующие строки.
Мы свели игру 2 x 9 к игре 2 x 3.
Так как игроки выбирают свои чистые стратегии случайным образом, то выигрыш игрока I будет случайной величиной. В этом случае игрок I должен выбрать свои смешанные стратегии так, чтобы получить максимальный средний выигрыш.
Аналогично, игрок II должен выбрать свои смешанные стратегии так, чтобы минимизировать математическое ожидание игрока I.
В матрице присутствуют отрицательные элементы. Для упрощения расчетов добавим к элементам матрицы (16). Такая замена не изменит решения игры, изменится только ее цена (по теореме фон Неймана).

3. Находим решение игры в смешанных стратегиях.
Математические модели пары двойственных задач линейного программирования можно записать так:
найти минимум функции F(x) при ограничениях (для игрока II):
6x₁ ≥ 1
x₁+17x₂ ≥ 1
4x₁+2x₂ ≥ 1
F(x) = x₁+x₂ → min
найти максимум функции Z(y) при ограничениях (для игрока I):
6y₁+y₂+4y₃ ≤ 1
17y₂+2y₃ ≤ 1
Z(y) = y₁+y₂+y₃ → max
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
Определим максимальное значение целевой функции Z(Y) = y₁+y₂+y₃ при следующих условиях-ограничений.
6y₁+y₂+4y₃≤1
17y₂+2y₃≤1
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
6y₁+y₂+4y₃+y₄ = 1
17y₂+2y₃+y₅ = 1
Решим систему уравнений относительно базисных переменных: y₄, y₅
Полагая, что свободные переменные равны 0, получим первый опорный план:
Y0 = (0,0,0,1,1)

Базис	B	y₁	y₂	y₃	y₄	y₅
y₄
y₅
Z(Y0)		-1	-1	-1

Переходим к основному алгоритму симплекс-метода.
Итерация №0.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
В качестве ведущего выберем столбец, соответствующий переменной y₃, так как это наибольший коэффициент по модулю.
Вычислим значения D_i по строкам как частное от деления: b_i / a_i3
и из них выберем наименьшее:
min (1 : 4 , 1 : 2 ) = ¹/₄
Следовательно, 1-ая строка является ведущей.
Разрешающий элемент равен (4) и находится на пересечении ведущего столбца и ведущей строки.

Базис	B	y₁	y₂	y₃	y₄	y₅	min
y₄							¹/₄
y₅							¹/₂
Z(Y1)		-1	-1	-1

Формируем следующую часть симплексной таблицы. Вместо переменной y₄ в план 1 войдет переменная y₃.
Получаем новую симплекс-таблицу:

Базис	B	y₁	y₂	y₃	y₄	y₅
y₃	¹/₄	³/₂	¹/₄		¹/₄
y₅	¹/₂	-3	³³/₂		^-1/₂
Z(Y1)	¹/₄	¹/₂	^-3/₄		¹/₄

Итерация №1.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
В качестве ведущего выберем столбец, соответствующий переменной y₂, так как это наибольший коэффициент по модулю.
Вычислим значения D_i по строкам как частное от деления: b_i / a_i2
и из них выберем наименьшее:
min (¹/₄ : ¹/₄ , ¹/₂ : 16¹/₂ ) = ¹/₃₃
Следовательно, 2-ая строка является ведущей.
Разрешающий элемент равен (16¹/₂) и находится на пересечении ведущего столбца и ведущей строки.

Базис	B	y₁	y₂	y₃	y₄	y₅	min
y₃	¹/₄	³/₂	¹/₄		¹/₄
y₅	¹/₂	-3	16¹/₂		^-1/₂		¹/₃₃
Z(Y2)	¹/₄	¹/₂	^-3/₄		¹/₄

Формируем следующую часть симплексной таблицы. Вместо переменной y₅ в план 2 войдет переменная y₂.

Получаем новую симплекс-таблицу:

Базис	B	y₁	y₂	y₃	y₄	y₅
y₃	⁸/₃₃	¹⁷/₁₁			¹⁷/₆₆	^-1/₆₆
y₂	¹/₃₃	^-2/₁₁			^-1/₃₃	²/₃₃
Z(Y2)	³/₁₁	⁴/₁₁			⁵/₂₂	¹/₂₂

Конец итераций: индексная строка не содержит отрицательных элементов - найден оптимальный план
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.
Окончательный вариант симплекс-таблицы:

Базис	B	y₁	y₂	y₃	y₄	y₅
y₃	⁸/₃₃	¹⁷/₁₁			¹⁷/₆₆	^-1/₆₆
y₂	¹/₃₃	^-2/₁₁			^-1/₃₃	²/₃₃
Z(Y3)	³/₁₁	⁴/₁₁			⁵/₂₂	¹/₂₂

Оптимальный план можно записать так:
y₁ = 0, y₂ = ¹/₃₃, y₃ = ⁸/₃₃
Z(Y) = 1•0 + 1•¹/₃₃ + 1•⁸/₃₃ = ³/₁₁
Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи.
x₁=⁵/₂₂, x₂=¹/₂₂
Это же решение можно получить, применив теоремы двойственности.
Из теоремы двойственности следует, что X = C*A^-1.
Составим матрицу A из компонентов векторов, входящих в оптимальный базис.

A = (A₃, A₂) =

Определив обратную матрицу D = А^-1 через алгебраические дополнения, получим:

D = A^-1 =

¹⁷/₆₆	^-1/₆₆
^-1/₃₃	²/₃₃

Как видно из последнего плана симплексной таблицы, обратная матрица A^-1расположена в столбцах дополнительных переменных.
Тогда X = C*A^-1 =

(1, 1) x

¹⁷/₆₆	^-1/₆₆
^-1/₃₃	²/₃₃

= (⁵/₂₂;¹/₂₂)

Оптимальный план двойственной задачи равен:
x₁ = ⁵/₂₂, x₂ = ¹/₂₂
F(X) = 1*⁵/₂₂+1*¹/₂₂ = ³/₁₁
Цена игры будет равна g = 1/F(x), а вероятности применения стратегий игроков:
q_i = g*y_i; p_i = g*x_i.
Цена игры: g = 1 : ³/₁₁ = ¹¹/₃
p₁ = ¹¹/₃*⁵/₂₂ = ⁵/₆
p₂ = ¹¹/₃*¹/₂₂ = ¹/₆
Оптимальная смешанная стратегия игрока I:
P = (⁵/₆; ¹/₆)
q₁ = ¹¹/₃* = 0
q₂ = ¹¹/₃*¹/₃₃ = ¹/₉
q₃ = ¹¹/₃*⁸/₃₃ = ⁸/₉
Оптимальная смешанная стратегия игрока II:
Q = (0; ¹/₉; ⁸/₉)
Поскольку ранее к элементам матрицы было прибавлено число (16), то вычтем это число из цены игры.
3²/₃ - 16 = -12¹/₃
Цена игры: v=^-37/₃
4. Проверим правильность решения игры с помощью критерия оптимальности стратегии.
∑a_ijq_j ≤ v
∑a_ijp_i ≥ v
M(P₁;Q) = (-10*0) + (-15*¹/₉) + (-12*⁸/₉) = -12.333 = v
M(P₂;Q) = (-16*0) + (1*¹/₉) + (-14*⁸/₉) = -12.333 = v
M(P;Q₁) = (-10*⁵/₆) + (-16*¹/₆) = -11 ≥ v
M(P;Q₂) = (-15*⁵/₆) + (1*¹/₆) = -12.333 = v
M(P;Q₃) = (-12*⁵/₆) + (-14*¹/₆) = -12.333 = v
Все неравенства выполняются как равенства или строгие неравенства, следовательно, решение игры найдено верно.
Поскольку из исходной матрицы были удалены и столбцы, то найденные векторы вероятности можно записать в виде:
P(⁵/₆,¹/₆)
Q(0,0,0,0,0,0,¹/₉,⁸/₉,0)

б)

Рассматриваем игру, после сведения ее к игре 2x3

-10	-15	-12
-16		-14

Находим решение игры в смешанных стратегиях.
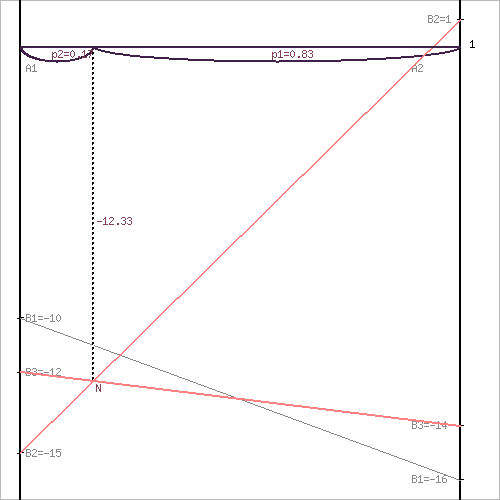
Решим задачу геометрическим методом, который включает в себя следующие этапы:
1. В декартовой системе координат по оси абсцисс откладывается отрезок, длина которого равна 1. Левый конец отрезка (точка х = 0) соответствует стратегии A₁, правый - стратегии A₂ (x = 1). Промежуточные точки х соответствуют вероятностям некоторых смешанных стратегий S₁ = (p₁,p₂).
2. На левой оси ординат откладываются выигрыши стратегии A₁. На линии, параллельной оси ординат, из точки 1 откладываются выигрыши стратегии A₂.
Решение игры (2 x n) проводим с позиции игрока A, придерживающегося максиминной стратегии. Доминирующихся и дублирующих стратегий ни у одного из игроков нет.
Выделяем нижнюю границу выигрыша B₂NB₃. Максиминной оптимальной стратегии игрока A соответствует точка N, лежащая на пересечении прямых B₂B₂ и B₃B₃, для которых можно записать следующую систему уравнений:
y = -15 + (1 - (-15))p₂
y = -12 + (-14 - (-12))p₂
Откуда
p₁ = ⁵/₆
p₂ = ¹/₆
Цена игры, y = ^-37/₃
Теперь можно найти минимаксную стратегию игрока B, записав соответствующую систему уравнений, исключив стратегию B₁, которая дает явно больший проигрыш игроку B, и, следовательно, q₁ = 0.
-15q₂-12q₃ = y
q₂-14q₃ = y
q₂+q₃ = 1
или
-15q₂-12q₃ = ^-37/₃
q₂-14q₃ = ^-37/₃
q₂+q₃ = 1
Решая эту систему, находим:
q₂ = ¹/₉.
q₃ = ⁸/₉.

Ответ:
Цена игры: y = ^-37/₃, векторы стратегии игроков:
Q(0, ¹/₉, ⁸/₉), P(⁵/₆, ¹/₆)
4. Проверим правильность решения игры с помощью критерия оптимальности стратегии.
∑a_ijq_j ≤ v
∑a_ijp_i ≥ v
M(P₁;Q) = (-10*0) + (-15*¹/₉) + (-12*⁸/₉) = -12.333 = v
M(P₂;Q) = (-16*0) + (1*¹/₉) + (-14*⁸/₉) = -12.333 = v
M(P;Q₁) = (-10*⁵/₆) + (-16*¹/₆) = -11 ≥ v
M(P;Q₂) = (-15*⁵/₆) + (1*¹/₆) = -12.333 = v
M(P;Q₃) = (-12*⁵/₆) + (-14*¹/₆) = -12.333 = v
Все неравенства выполняются как равенства или строгие неравенства, следовательно, решение игры найдено верно.
Поскольку из исходной матрицы были удалены и столбцы, то найденные векторы вероятности можно записать в виде:
P(⁵/₆,¹/₆)
Q(0,0,0,0,0,0,¹/₉,⁸/₉,0)

⇐ Предыдущая 123 Следующая ⇒