
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Принятие решения в условиях риска
1. Принятие решения в условиях риска
1.1 Классические критерии
а) Минимаксный критерий:
Еоптим = min max (eij)
е1 = -8 е3 = -4 е5 = -2 е7 = -2
е2 = -5 е4 = -3 е6 = -3
Еоптим = min { -8; -5; -4; -3; -2; -3; -2} = -8 следовательно выбираем стратегию Е1
б) Критерий Байеса – Лапласа:
Еоптим = max eir, где eir = 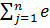 ij qj
ij qj
q1 = 0,1 q3 = 0,2 q5= 0,1 q7= 0,05 q9= 0,01 q11= 0,04
q2 = 0,2 q4 = 0,05 q6= 0,15 q8= 0,02 q10= 0,03 q12= 0,05
ei1 = -28*0,1+(-30)*0,2+(-46)*0,2+(-8)*0,05+(-44)*0,1+(-19)*0,15+(-8)*0,05+ (-21)*0,02+(-32)*0,01+(-22)*0,03+(-43)*0,04+(-23)*0,05= -30,32
ei2 = -25*0,1+(-12)*0,2+(-22)*0,2+(-46)*0,05+(-5)*0,1+(-15)*0,15+(-14)*0,05+ (-8)*0,02+(-43)*0,01+(-21)*0,03+(-40)*0,04+(-46)*0,05= -20,17
ei3 = -41*0,1+(-26)*0,2+(-48)*0,2+(-30)*0,05+(-46)*0,1+(-4)*0,15+(-28)*0,05+ (-25)*0,02+(-25)*0,01+(-20)*0,03+(-16)*0,04+(-38)*0,05= -30,89
ei4= (-12)*0,1+(-46)*0,2+(-6)*0,2+(-31)*0,05+(-3)*0,1+(-33)*0,15+(-9)*0,05+ (-41)*0,02+(-18)*0,01+(-39)*0,03+(-41)*0,04+(-43)*0,05= -24,81
ei5= -6*0,1+(-30)*0,2+(-17)*0,2+(-24)*0,05+(-35)*0,1+(-20)*0,15+(-20)*0,05+ (-27)*0,02+(-45)*0,01+(-2)*0,03+(-19)*0,04+(-7)*0,05= -20,86
ei6 = -26*0,1+(-28)*0,2+(-42)*0,2+(-6)*0,05+(-3)*0,1+(-27)*0,15+(-48)*0,05+ (-5)*0,02+(-9)*0,01+(-14)*0,03+(-3)*0,04+(-10)*0,05= -24,88
ei7= -13*0,1+(-47)*0,2+(-18)*0,2+(-9)*0,05+(-48)*0,1+(-22)*0,15+(-26)*0,05+ (-33)*0,02+(-33)*0,01+(-6)*0,03+(-2)*0,04+(-48)*0,05= -27,8
Еоптим = min { -30,22; -20,17; -30,89; -24,81; -20,86; -24,88; -27,8} = -20,17
следовательно необходимо выбрать стратегию Е2
в) Критерий Сэвиджа:
Еоптим= mini [ maxj(maxieij-eij)]
aj = maxi eij
a1=-6 a4=-6 a7=-8 a10=-2
a2=-12 a5=-3 a8=-5 a11=-2
a3=-6 a6=-4 a9=-9 a12=-7
Кij= maxieij-eij= aj-eij
Составим матрицу К1 состоящую из элементов Кij
bi =maxi(max eij-eij) = maxj Kij
b1=41 b3=43 b5=36 b1=45
b2=40 b4=39 b6=40
Еоптим= min bi= min {41; 40; 43; 39; 36; 40; 45}= 36 следовательно необходимо выбрать стратегию Е5
1.2 Производные критерии
а) Критерий Гурвица:
Еоптим= maxi[c minj eij+(1-c) maxi eij]
Возьмем с=0,3 следовательно 1-с=0,7
| ai= minj eij | bi= maxj eij |
| a1=-46 | b1=-8 |
| a2=-46 | b2=-5 |
| a3=-48 | b3=-4 |
| a4=-46 | b4=-3 |
| a5=-35 | b5=-2 |
| a6=-48 | b6=-3 |
| a7=-48 | b7=-2 |
ki=c minjeij+(1-c) maxjeij=cai+(1-c)bi
k1=0,3*(-46)+0,7*(-8)=-19,4
k2=0,3*(-46)+0,7*(-5)=-17,3
k3=0,3*(-48)+0,7*(-4)=-17,2
k4=0,3*(-46)+0,7*(-3)=-15,9
k5=0,3*(-35)+0,7*(-2)=-11,9
k6=0,3*(-48)+0,7*(-3)=-16,5
k7=0,3*(-48)+0,7*(-2)=-15,8
Еоптим= maxiki=max{-19,4; -17,3; -17,2; -15.9; -11,9; -16,5; -15,8}= -11,9 следовательно необходимо выбрать стратегию Е5
б) Критерий Ходжа-Лемана:
Еоптим= max [λ 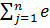 ijqj+(1-λ) minjeij]
ijqj+(1-λ) minjeij]
Возьмем λ=0,7 следовательно 1-λ=0,3
qj возьмем равным qj из критерия Байеса-Лапласа, то есть
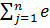 ij qj=eir
ij qj=eir
ai= λ* eir= 0,7* eir
a1=-21,224 a3=-21,623 a5=-14,602 a7=-19, 46
a2=-14,119 a4=-17,367 a6=-17,416
bi=0,3* minj eij
b1=-13,8 b3=-14,4 b5=-10,5 b7=-14,4
b2=-13,8 b4=-13,8 b6=-14,4
ki= ai + bi
k1=-35,024 k3=-36,023 k5=-25,102 k7=-33,86
k2=-27,919 k4=-31,167 k6=-31,816
Еоптим= maxiki= max {-35,024; -27,919; -36,023; -31,167; -25,102; -31,816; -33,86}= -25,102 следовательно необходимо выбирать стратегию Е5
в) Критерий Гермейера:
Еоптим= maxi minj eijqj
Возьмем qj равным qj из критерия Байеса-Лапласа
aij= eij*qj
Составим матрицу А, состоящую из элементов aij :
| -2,8 | -6 | -9,2 | -0,4 | -4,4 | -2,85 | -0,4 | -0,42 | -0,32 | -0,66 | -1,72 | -1,15 | |
| -2,5 | -2,4 | -4,4 | -2,3 | -0,5 | -2,25 | -0,7 | -0,16 | -0,43 | -0,63 | -1,6 | -2,3 | |
| -4,1 | -5,2 | -9,6 | -1,5 | -4,6 | -0,6 | -1,4 | -0,5 | -0,25 | -0,6 | -0,64 | -1,9 | |
| -1,2 | -9,2 | -1,2 | -1,55 | -0,3 | -4,95 | -0,45 | -0,82 | -0,18 | -1,17 | -1,64 | -2,15 | |
| -0,6 | -6 | -3,4 | -1,2 | -3,5 | -3 | -1 | -0,54 | -0,45 | -0,06 | -0,76 | -0,35 | |
| -2,6 | -5,6 | -8,4 | -0,3 | -0,3 | -4,05 | -2,4 | -0,1 | -0,09 | -0,42 | -0,12 | -0,5 | |
| -1,3 | -9,4 | -3,6 | -0,45 | -4,8 | -3,3 | -1,3 | -0,66 | -0,33 | -0,18 | -0,08 | -2,4 |
bi= minj aij
b1=-9,2 b3=-9,6 b5=-3,5 b7=-9,4
b2=-4,4 b4=-9,2 b6=-8,4
Еоптим= maxibi= max {-9,2; -4,4; -9,6; -9,2; -3,5; -8,4; -9,4}= -3,5 следовательно необходимо выбирать стратегию Е5
г) BL (MM):
Возьмем qj= 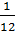 , j=1,12
, j=1,12
Определим ei0 j0= max min eij
Пусть E=1 – уровень допустимого риска
ei0 j0= max {-46; -46; -48; -46; -45; -48; -48}= -45
ei0 j0= -45; j0=9, i0=5
maxi ei0j=-2
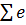 ijqj ijqj
| minj eij | ei0 j0 – minj eij | maxj eij | maxj eij-maxj ei0j | |
| E1 | -27 | -46 | -8 | -6 | |
| E2 | -24,75 | -46 | -5 | -3 | |
| E3 | -28,92 | -48 | -4 | -2 | |
| E4 | -26,8 | -46 | -3 | -1 | |
| E5 | -21 | -45 | -2 | ||
| E6 | -18,42 | -48 | -3 | -1 | |
| E7 | -25,42 | -48 | -2 |
Определим множество согласия, являющиеся подмножеством индексов {1,…,m} I1={i|i ϵ {1,…,m}˄ei0 j0-min eij≤E}
I1={1;2;4;5}
Также рассматриваем некоторое выигрышное множество
I2: ={i|i ϵ {1,…,m}˄maxj eij-maxj ei0j ≥ ei0 j0-minj eij= Ei}
I2={5,7}
Оптимальным в смысле BL (MM) – критерия будут решения из множества
Е0={ei0 ϵ E˄ ei0 = max 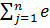 ijqj} i=I1˄I2
ijqj} i=I1˄I2
I1˄I2={5}
E0=E5 следовательно стоит выбрать стратегию Е5
д) Критерий произведений:
Еоптим=maxi  ij
ij
 ij ij
| |
| E1 | 3,02*1016 |
| E2 | 0,42*1016 |
| E3 | 6,01*1016 |
| E4 | 0,46*1016 |
| E5 | 0,03*1016 |
| E6 | 0,001*1016 |
| E7 | 0,17*1016 |
Еоптим= max {3,02*1016; 0,42*1016; 6,01*1016; 0,46*1016; 0,03*1016; 0,001*1016; 0,17*1016} = 6,01*1016 следовательно необходимо выбрать стратегию Е3
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|