восьмеричной системой счисления называется позиционная система счисления с основанием8.

восьмеричной системой счисления называется позиционная система счисления с основанием8.

Для записи чисел в восьмеричной системе счисления используются цифры: 0, 1, 2, 3, 4, 5, 6, 7.

Для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.

Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю. Исходное число в восьмеричной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.

Пример:

Переведём восьмеричное число 15436₈ в десятичную систему счисления.

15436₈=1⋅8⁴+5⋅8³+4⋅8²+3⋅8¹+6⋅8⁰=6942₁₀

Пример:

Переведём десятичное число 94 в восьмеричную систему счисления.

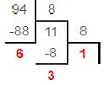
94₁₀=136₈

Шестнадцатеричной системой счисления называется позиционная система счисления с основанием16.

Для записи чисел в шестнадцатеричной системе счисления используются цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и латинские буквы A, B, C, D, E, F. Буквы A, B, C, D, E, F имеют значения 10₁₀, 11₁₀, 12₁₀, 13₁₀, 14₁₀, 15₁₀.

Для перевода целого десятичного числа в шестнадцатеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 16 до тех пор, пока не получим частное, равное нулю. Исходное число в системе счисления составляется последовательной записью полученных остатков, начиная с последнего.

Пример:

Переведём шестнадцатеричное число 2A7 в десятичное. В соответствии с вышеуказанными правилом представим его в виде суммы степеней с основанием 16:

2A716=2⋅162+10⋅161+7⋅160=512+160+7=679.

Пример:

Переведём десятичное число 158 в шестнадцатеричную систему счисления.

15810=9E16.

Для перевода числа из любой позиционной системы счисления в десятичную необходима использовать развернутую формулу числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами.

Для перевода целых чисел десятичной системы счисления в число любой системы счисления последовательно выполняют деление нацело на основание системы счисления, пока не получат нуль. Числа, которые возникают как остаток от деления на основание системы счисление, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.

⇐ Предыдущая 1 23