Двоичной системой счисления называется позиционная система счисления с основанием2.

Позиционными называют такие системы счисления, в которых значение каждого знака (цифры) в записи любого числа зависит от расположения (позиции) этого знака в числе. Количество цифр, используемых для записи чисел в позиционной системе счисления, называется ееоснованием.

Мы используем позиционную десятичную систему счисления. Основанием этой системы является число 10.

Для записи любого числа в десятичной системе счисления используют десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Комбинируя эти цифры, можно записывать любые числа.

Например, цифры числа 737 в десятичной системе счисления являются коэффициентами его записи в виде суммы степеней числа 10:

737=7⋅10²+3⋅10¹+7⋅10⁰=7⋅100+3⋅10+7⋅1

Из этого примера видно, что цифра 7 в зависимости от своей позиции в этом числе означает и 7 сотен, и 7 единиц, а цифра 3 означает три десятка.

Пример:

Рассмотрим десятичное число 13456,7. Его свёрнутая форма записи настолько привычна, что мы не замечаем, как в уме переходим к развернутой записи, умножая цифры числа на «веса» разрядов и складывая полученные произведения:

1⋅10⁴+3⋅10³+4⋅10²+5⋅10¹+6⋅10⁰+7⋅10⁻¹^.

Теория:

Для кодирования информации в компьютере вместо привычной десятичной системы счисления используется двоичная система счисления.

Двоичной системой счисления люди начали пользоваться очень давно. Древние племена Австралии и островов Полинезии использовали эту систему в быту. Так, полинезийцы передавали необходимую информацию, выполняя два вида ударов по барабану: звонкий и глухой. Это было примитивное представление двоичной системы счисления.

Двоичной системой счисления называется позиционная система счисления с основанием2.

Для записи чисел в ней использовали только две цифры: 0 и 1.

Для обозначения системы счисления, в которой представляется число, используют нижний индекс, указывающий основание системы. Например, 110112 — число в двоичной системе счисления.

Цифры в двоичном числе являются коэффициентами его представления в виде суммы степеней с основанием 2, например:

101₂=1⋅2²+0⋅2¹+1⋅2⁰.

В десятичной системе счисления это число будет выглядеть так:

101₂=4+0+1=5.

Для перевода целого десятичного числа в двоичную систему счисления нужно последовательно выполнять деление данного числа и получаемых целых частных на 2 до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.

Пример:

Переведём десятичное число 13 в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) можно изобразить так:

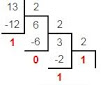
Получили 13₁₀=1101₂_.

Пример:

Если десятичное число достаточно большое, то более удобен следующий способ записи рассмотренного выше алгоритма:

224₁₀=11100000₂.

⇐ Предыдущая 123 Следующая ⇒