
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Опорный конспект «СВОЙСТВА ФУНКЦИИ»
Опорный конспект «СВОЙСТВА ФУНКЦИИ»
Опр.1. Функцию у= f(x) называют возрастающейна множестве Х , если для любых точек x1 и x2 из множества Х, таких, что x1 < x2, выполняется неравенство f (x1) < f (x2). (Функция возрастает, если большему значению аргумента соответствует большее значение функции)
Опр.2. Функцию у= f(x) называют убывающей на множестве Х , если для любых точек x1 и x2 из множества Х, таких , что x1 < x2, выполняется неравенство f (x1 ) > f(x2). (Функция убывает, если большему значению аргумента соответствует меньшее значение функции)
Термины «возрастающая функция», «убывающая функция» объединяют общим названием
 монотонная функция
монотонная функция
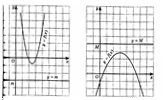
Опр.3. Функцию у= f(x)называют ограниченной снизу на множестве Х, если все значения этой функции на множестве Х больше некоторого числа, т.е., если существует такое число m, что для любого значения х выполняется неравенство f(x) > m
Опр.4. Функцию у= f(x) называют ограниченной сверху на множестве Х, если все значения этой функции на множестве Х меньше некоторого числа , т.е. , если существует такое число М , что для любого значения х выполняется неравенство f(x) < М
Если функция ограничена и снизу и сверху на всей области определения, то ее называют ограниченной.
Опр.5. Число m называют наименьшим значениемфункции у= f(x) на множестве Х , если:
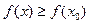 1) во множестве Х существует такая точка x0 , что f(x0) = m
1) во множестве Х существует такая точка x0 , что f(x0) = m
2) для любого значения х из множества Х выполняется неравенство
Опр.6. Число М называют наибольшим значением функции у= f(x) на множестве Х, если:
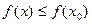 1) во множестве Х существует такая точка, что f(x0) = М
1) во множестве Х существует такая точка, что f(x0) = М
2) для любого значения х из множества Х выполняется неравенство
Утв.1. Если у функции существует yнаиб,то она ограничена сверху
Утв.2. Если у функции существует yнаим, то она ограничена снизу.
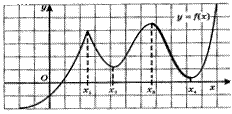
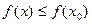 Опр.7. Точку x0 называют точкой максимума функции у= f(x), если у этой точки существует окрестность, для всех точек которой (кроме самой точки x0) выполняется неравенство
Опр.7. Точку x0 называют точкой максимума функции у= f(x), если у этой точки существует окрестность, для всех точек которой (кроме самой точки x0) выполняется неравенство
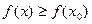
 Опр.8. Точку x0 называют точкой минимума функции у= f(x), если у этой точки существует окрестность, для всех точек которой (кроме самой точки x0) выполняется неравенство
Опр.8. Точку x0 называют точкой минимума функции у= f(x), если у этой точки существует окрестность, для всех точек которой (кроме самой точки x0) выполняется неравенство
Точки максимума и минимума объединяют общим названием – точки экстремума
Опр.9. Функция выпукла вниз на промежутке Х, если, соединив любые две точки ее графика (с абсциссами из Х) отрезком, мы обнаружим, что соответствующая часть графика лежит ниже проведенного отрезка.
Опр.10. Функция выпукла вверх на промежутке Х, если, соединив любые две точки ее графика (с абсциссами из Х) отрезком, мы обнаружим, что соответствующая часть графика лежит выше проведенного отрезка.
Непрерывность функции на отрезке Х– означает, что график функции на данном промежутке не имеет точек разрыва
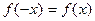 Опр. 11. Функцию у= f(x) называют четной, если для любого значения х из множества Х выполняется равенство
Опр. 11. Функцию у= f(x) называют четной, если для любого значения х из множества Х выполняется равенство
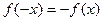 Опр.12. Функцию у= f(x) называют нечетной, если для любого значения х из множества Х выполняется равенство
Опр.12. Функцию у= f(x) называют нечетной, если для любого значения х из множества Х выполняется равенство
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|