Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

Приведём другое решение.. Решение.. Решение.. Решение.. Решение.

Приведём другое решение.

Пусть b — первый член, а q — знаменатель прогрессии. Сумма первого и второго членов геометрической прогрессии отличается от суммы второго и третьего в q раз, поэтому q = 3. Тогда b + 3b = 48, поэтому b = 12. Таким образом, искомые члены прогрессии равны 12, 36 и 108.

Ответ: 2550100

Источник: Банк заданий ФИПИ

5. 321377

Гео­мет­ри­че­ская про­грес­сия за­да­на усло­ви­ем Най­ди­те сумму пер­вых её 4 чле­нов.

Решение.

Найдём зна­ме­на­тель гео­мет­ри­че­ской прогрессии:

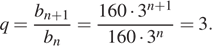
Первый член дан­ной про­грес­сии равен 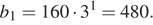Сумма пер­вых 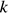чле­нов гео­мет­ри­че­ской про­грес­сии может быть най­де­на по фор­му­ле:

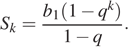
Необходимо найти 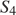, имеем:

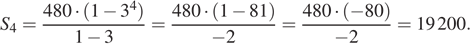
Ответ: 19 200.

Ответ: 19200

6.

Выписаны пер­вые не­сколь­ко чле­нов гео­мет­ри­че­ской прогрессии: 17, 68, 272, ... Най­ди­те её четвёртый член.

Решение.

Найдём зна­ме­на­тель гео­мет­ри­че­ской прогрессии:

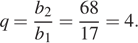
Четвёртый член про­грес­сии равен

Ответ: 1088.

Ответ: 1088

7.

Вы­пи­са­но не­сколь­ко по­сле­до­ва­тель­ных чле­нов гео­мет­ри­че­ской про­грес­сии: … ; 150 ; x ; 6 ; 1,2 ; … Най­ди­те член про­грес­сии, обо­зна­чен­ный бук­вой x.

Решение.

Найдем зна­ме­на­тель гео­мет­ри­че­ской прогрессии: 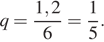Поэтому,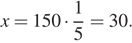

Ответ: 30.

Ответ: 30

8.

Выписаны пер­вые не­сколь­ко чле­нов гео­мет­ри­че­ской прогрессии: −1024; −256; −64; … Най­ди­те сумму пер­вых 5 её членов.

Решение.

Найдём зна­ме­на­тель гео­мет­ри­че­ской прогрессии:

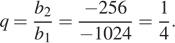
Найдём четвёртый и пятый члены про­грес­сии:

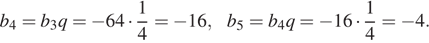
Сумма пер­вых пяти пер­вых чле­нов про­грес­сии равна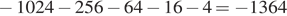

Ответ: −1364.

Ответ: -1364

-1364

Источник: МИОО: Ди­а­гно­сти­че­ская ра­бо­та по ма­те­ма­ти­ке 17.04.2014 ва­ри­ант МА90601

9.

Гео­мет­ри­че­ская про­грес­сия за­да­на усло­ви­ем 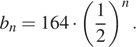Най­ди­те сумму пер­вых её 4 чле­нов.

Решение.

Найдём зна­ме­на­тель гео­мет­ри­че­ской прогрессии:

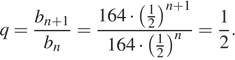
Первый член дан­ной про­грес­сии равен 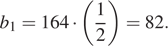Сумма пер­вых 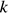чле­нов гео­мет­ри­че­ской про­грес­сии может быть най­де­на по фор­му­ле:

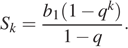
Необходимо найти 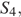имеем:

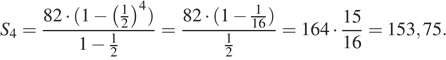
Ответ: 153,75.

Ответ: 153,75

153,75

Источник: Банк заданий ФИПИ

10.341197

Вы­пи­са­но не­сколь­ко по­сле­до­ва­тель­ных чле­нов гео­мет­ри­че­ской про­грес­сии: … ; 1,75; x; 28 ; −112; … Най­ди­те член про­грес­сии, обо­зна­чен­ный бук­вой x.

Решение.

Найдем зна­ме­на­тель гео­мет­ри­че­ской прогрессии: 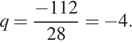Поэтому,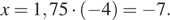

Ответ: −7.

Ответ: -7

-7

Источник: Банк заданий ФИПИ

11.

Дана гео­мет­ри­че­ская про­грес­сия (b_n), для ко­то­рой b₅ = −14, b₈ = 112. Най­ди­те зна­ме­на­тель прогрессии.

Решение.

Член гео­мет­ри­че­ской про­грес­сии с но­ме­ром n вы­чис­ля­ет­ся по фор­му­ле 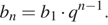Зная, что b₅ = −14 и b₈ = 112, по­лу­ча­ем си­сте­му уравнений. Решим систему, раз­де­лив вто­рое урав­не­ние на первое:

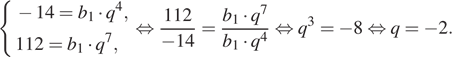
Ответ: −2.

Ответ: -2

-2

Источник: Банк заданий ФИПИ

12.

Гео­мет­ри­че­ская про­грес­сия за­да­на усло­ви­ем b₁ = −7, b_{n + 1} = 3b_n. Най­ди­те сумму пер­вых 5 её членов.

Решение.

Найдём зна­ме­на­тель гео­мет­ри­че­ской прогрессии:

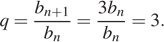
Сумма пер­вых 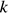чле­нов гео­мет­ри­че­ской про­грес­сии может быть най­де­на по фор­му­ле:

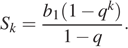
Необходимо найти 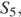имеем:

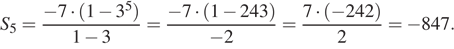
Ответ: −847.

Ответ: -847

-847

Источник: Банк заданий ФИПИ

13.

Дана гео­мет­ри­че­ская про­грес­сия (b_n), зна­ме­на­тель ко­то­рой равен 2, а b₁ = 16. Най­ди­те b₄.

Решение.

Член гео­мет­ри­че­ской про­грес­сии с но­ме­ром n можно найти по фор­му­ле b_n = b₁ · q^{n − 1}. В нашем слу­чае n = 4:

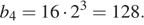
Ответ: 128.

Ответ: 128

Источник: Банк заданий ФИПИ

14. Задание 11 № 341217

Дана гео­мет­ри­че­ская про­грес­сия (b_n), зна­ме­на­тель ко­то­рой равен 5, а 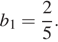Най­ди­те сумму пер­вых 6 её членов.

Решение.

Сумма n пер­вых чле­нов гео­мет­ри­че­ской про­грес­сии да­ёт­ся формулой

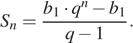
По условию, 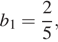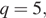от­ку­да получаем

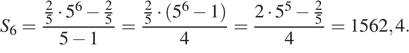
Ответ: 1562,4.

Ответ: 1562,4

1562,4

Источник: Банк заданий ФИПИ

15.

Вы­пи­са­ны пер­вые не­сколь­ко чле­нов гео­мет­ри­че­ской про­грес­сии: − 256; 128; − 64; … Най­ди­те сумму пер­вых семи её членов.

Решение.

Найдём зна­ме­на­тель гео­мет­ри­че­ской прогрессии:

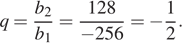
Сумма пер­вых 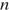чле­нов гео­мет­ри­че­ской про­грес­сии может быть най­де­на по формуле:

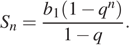
Необходимо найти 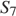, имеем:

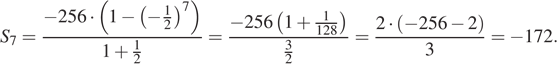
Ответ: −172.

Ответ: -172

-172

Источник: Банк заданий ФИПИ

16. 353212

Дана гео­мет­ри­че­ская про­грес­сия (b_n), для ко­то­рой b₃ = , b₆ = -196. Най­ди­те зна­ме­на­тель прогрессии.

Решение.

Член гео­мет­ри­че­ской про­грес­сии с но­ме­ром n вы­чис­ля­ет­ся по фор­му­ле 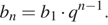Зная, что b₃ = и b₆ = -196, по­лу­ча­ем си­сте­му уравнений. Решим систему, раз­де­лив вто­рое урав­не­ние на первое:

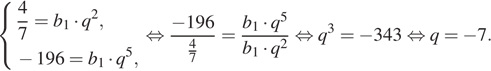
Ответ: −7.

Ответ: -7

-7

17. № 353420

Гео­мет­ри­че­ская про­грес­сия за­да­на усло­ви­ем b₁ = −3, b_{n + 1} = 6b_n. Най­ди­те сумму пер­вых 4 её членов.

Решение.

Найдём зна­ме­на­тель гео­мет­ри­че­ской прогрессии:

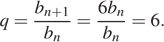
Сумма пер­вых 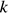чле­нов гео­мет­ри­че­ской про­грес­сии может быть най­де­на по фор­му­ле:

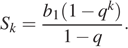
Необходимо найти 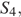имеем:

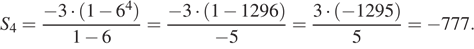
Ответ: −777.

Ответ: -777

-777

18. 353437

Вы­пи­са­но не­сколь­ко по­сле­до­ва­тель­ных чле­нов гео­мет­ри­че­ской про­грес­сии: … ; -12 ; x ; -3 ; 1,5 ; … Най­ди­те член про­грес­сии, обо­зна­чен­ный бук­вой x.