
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическое занятие № 1. Указание для задания: В случае получения неопределенности воспользуйтесь алгоритмом
Практическое занятие № 1
Тема: «Вычисление предела функции в точке».
Цель:1.Сформировать навык вычисления пределов функции в точке.
2. Способствовать развитию навыков самостоятельного применения знаний при вычислении пределов функции.
3. Способствовать привитию сознательного приобретения новых знаний по теме.
Теоретические сведения к практической работе:
Число А называют пределом функцииf(x) при 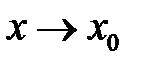 (и пишут
(и пишут 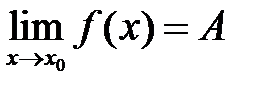 ), если для любого
), если для любого 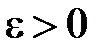 найдется число
найдется число 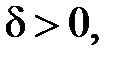 зависящее от , такое, что для всех
зависящее от , такое, что для всех 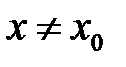 , удовлетворяющих условию
, удовлетворяющих условию 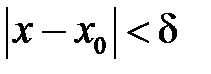 , выполняется неравенство
, выполняется неравенство 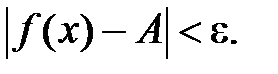
Теоремы о пределах:
1. 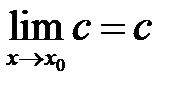 (c=const).
(c=const).
2. Если 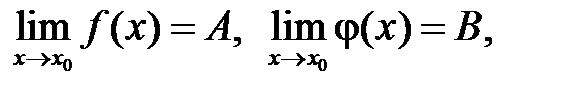 то:
то:
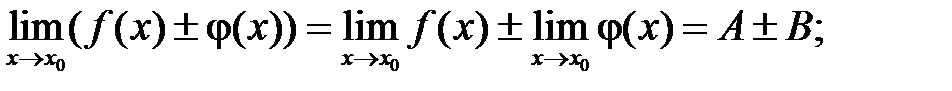
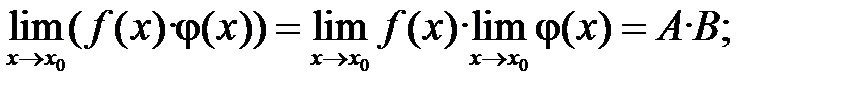
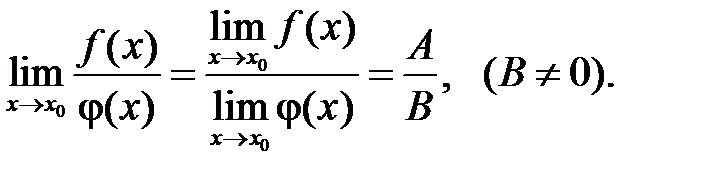
Часто при вычислении пределов какой-либо функции, непосредственное применение теорем о пределах не приводит к желаемой цели. Так, например, нельзя применять теорему о пределе дроби, если ее знаменатель стремится к нулю. Поэтому часто прежде, чем применять эти теоремы, необходимо тождественно преобразовать функцию, предел которой мы ищем.
Методические указания к выполнению заданий:
Указание для задания: В случае получения неопределенности воспользуйтесь алгоритмом

А) разложить числитель и знаменатель на множители, используя формулы сокращенного умножения:
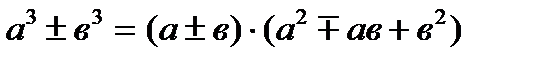
Б) разложить на множители и числитель и знаменатель по формуле ах2+bx+c=a(x-x1)(x-x2), где х1, х2 – корни уравнения.
В) домножить числитель и знаменатель на выражение сопряженное знаменателю, например:
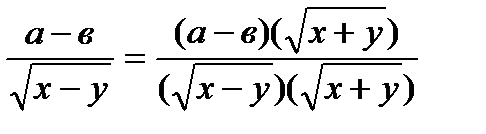
Задания для самостоятельного выполнения студентами:
| Вариант - 1 | Вариант - 2 |
| Найти пределы функций: | Найти пределы функций: |
1) 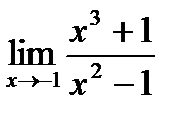 2)
2) 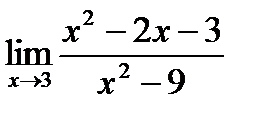 3)
3) 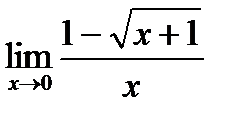 4)
4) 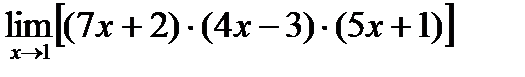 5)
5) 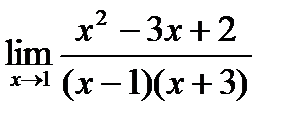 6)
6) 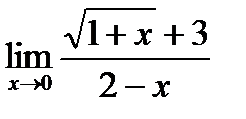 7)
7) 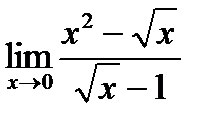 8)
8) 
| 1) 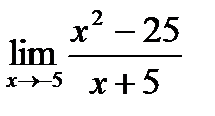 2)
2) 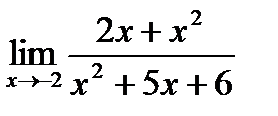 3)
3)  4)
4) 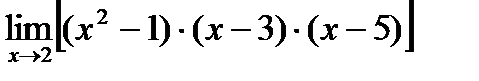 5)
5) 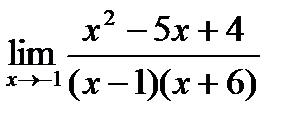 6)
6) 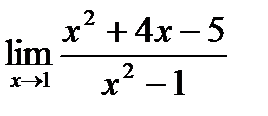 7)
7) 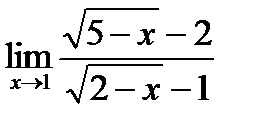 8)
8) 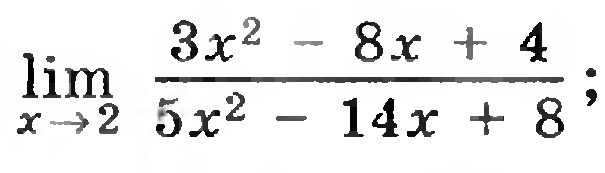
|
| Вариант - 3 | Вариант - 4 |
| Найти пределы функций: | Найти пределы функций: |
1) 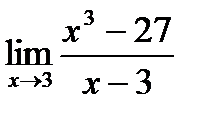 2)
2) 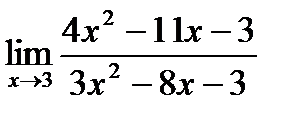 3)
3) 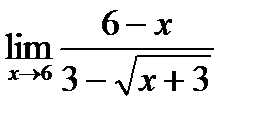 4)
4) 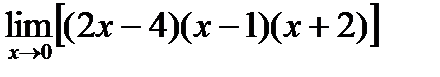 5)
5) 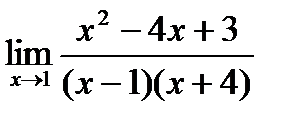 6)
6) 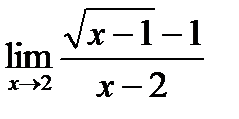 7)
7) 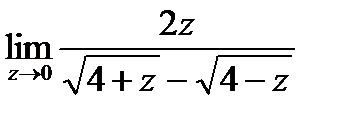 8)
8) 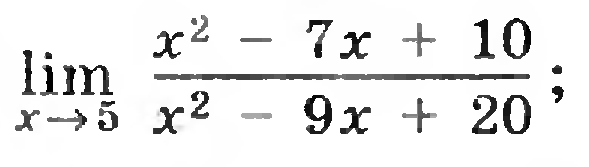
| 1) 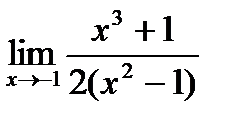 2)
2) 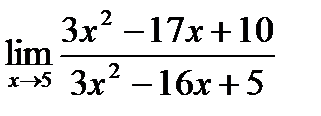 3)
3) 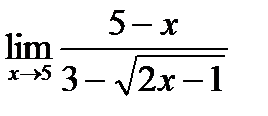 4)
4) 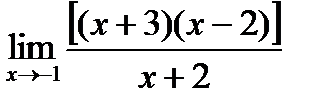 5)
5) 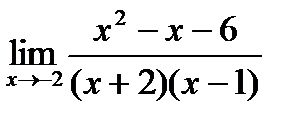 6)
6) 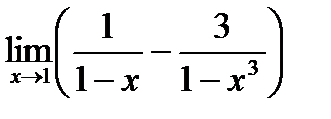 7)
7) 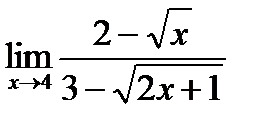 8)
8) 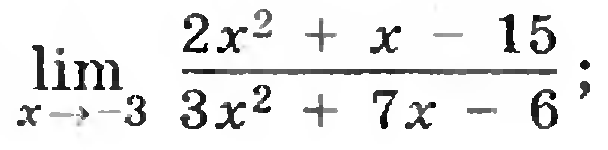
|
| Вариант - 5 | Вариант - 6 |
| Найти пределы функций: | Найти пределы функций: |
1) 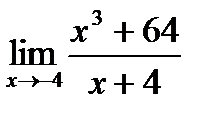 2)
2) 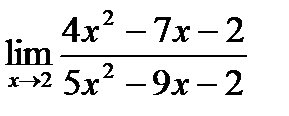 3)
3) 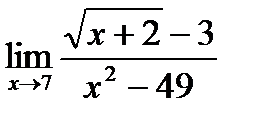 4)
4) 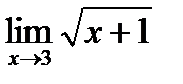 5)
5) 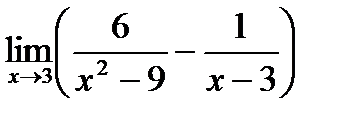 6)
6) 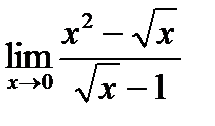 7)
7) 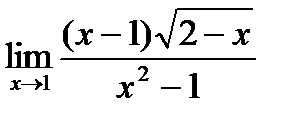 8)
8) 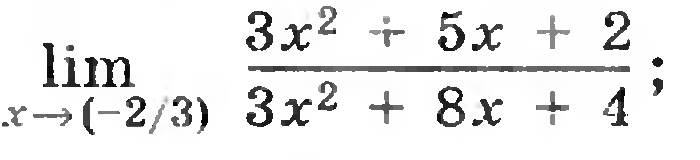
| 1) 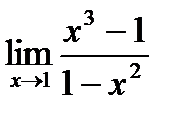 2)
2) 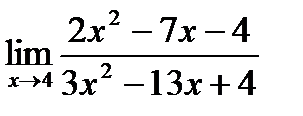 3)
3) 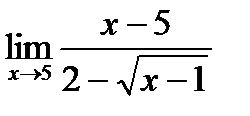 4)
4) 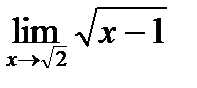 5)
5) 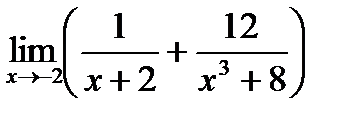 6)
6) 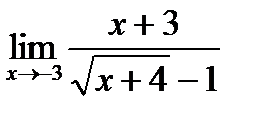 7)
7) 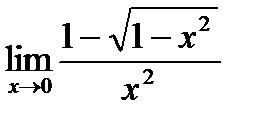 8)
8) 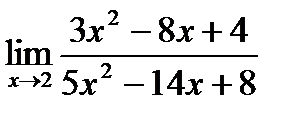
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|