Линейная регрессия.

Линейная регрессия.

Линейная регрессия — используемая в статистике регрессионная модель зависимости одной (объясняемой, зависимой) переменной от другой или нескольких других переменных (факторов, регрессоров, независимых переменных) с линейной функцией зависимости.

Пусть (X, У) — двумерная случайная величина, где X и Y — зависимые случайные величины. Оказывается возможным приближенное представление величины Y в виде линейной функции величины X:

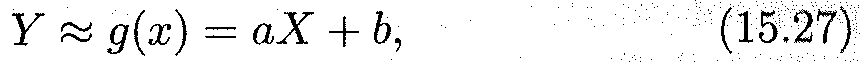
где а и b — параметры, подлежащие определению. Обычно эти величины определяются с помощью метода наименьших квадратов.

Определение 5.Функция (15.27) называется наилучшим приближением в смысле метода наименьших квадратов, если математическое ожидание

M[Y - g(Х)]² принимает наименьшее возможное значение. Функцию g(х) называют среднеквадратической регрессией Y на X.

ТЕОРЕМА Линейная средняя квадратическая регрессия Y на X имеет вид

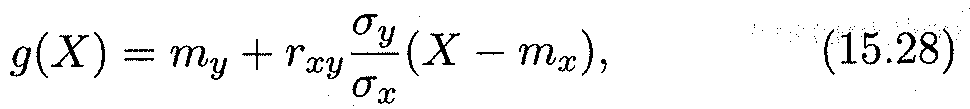
где r_x_y определяется формулой (15.25)

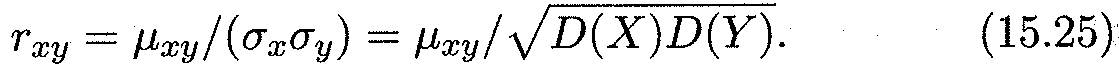m_y = M(Y) и т_х = М(Х) — математические ожидания соответственно случайных величин Y и X.

Коэффициент b = r_хуσ_у/σ_х называют коэффициентом регрессии Y на X, а прямую

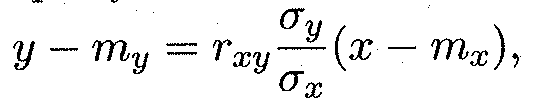
реализующую линейную зависимость (15.28) случайной величины Y от случайной величины X, называют прямой среднеквадратической регрессии Y на X. Поскольку зависимость (15.28) является приближенной, то существует погрешность этого приближения, называемая остаточной дисперсией:

Аналогичную форму записи имеет прямая среднеквадратическая регрессия X на Y:

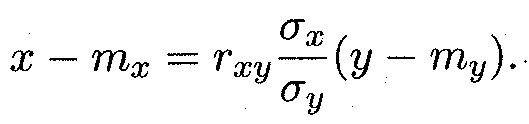
Пример 3. Найти линейную среднюю квадратическую регрессию и остаточную дисперсию случайной величины Yна случайную величину Xпо данным примеров 1 и 2.

РЕШЕНИЕ. Для двумерной случайной величины (X, Y), приведенной в примере 1, все необходимые числовые характеристики указаны в решении примера2: т_х= 2,03, т_у= 1,63, r_ху =-0,023, σ_х= √D(X)=0,793, σ_у= √D(Y) =0,483. Из уравнения(15.28) получаем искомое соотношение:

g(Х) =1,63 - 0,014(Х - 2,03).

Остаточная дисперсия рассчитывается по формуле (15.29):

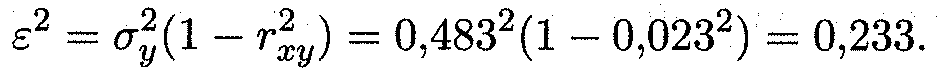Для оценки среднеквадратичной погрешности линейной регрессии обычно используют величину σ_у, в нашем случае она составляет σ_у = 0,483.

⇐ Предыдущая 1 23