Отрицание утверждений. Упражнения

Отрицание утверждений

Для примера возьмём (хоть мы его пока и не понимаем) определение интеграла Римана:

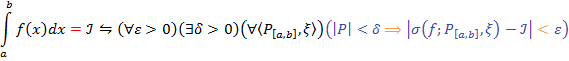
Общее правило отрицания какого-либо высказывания, как например, только что приведённого, состоит в следующем: заменяем все кванторы всеобщности кванторами существования, и наоборот, а последнее утверждение (в случае выше — выделенное лиловым цветом) заменяем его логическим отрицанием. Таким образом, отрицание утверждения выше выглядит так:

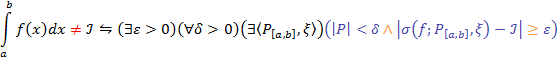
*Почему 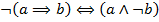— см. упражнения.

Упражнения

Формально к определению символов 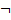, , 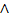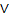и т.д. можно подойти с двух сторон: с точки зрения синтаксиса и с точки зрения семантики. Первое подразумевает их рассмотрение как «лингвистических» объектов, связывающих между собой некоторые высказывания (примерно так и мы определили их); второе — определение их как символов операций над высказываниями. Развивая второй подход, приводят так называемые таблицы истинности, которые связывают истинность составного высказывания (например, 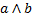) с истинностью их составляющих (истинностью 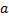и 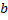). Вот эти таблицы
(1 — истина (true), 0 — ложь (false)):

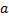
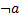
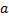
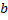
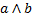
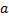
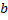
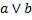
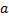
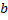
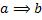
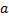
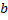
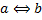
Формула (как, например, выражение ) называется тождественно истинной, если при всех оценках её составляющих ( 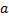, 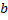и т.д.) она принимает значение 1.

№1. Пользуясь таблицами истинности, докажите теорему 1.1.1.

№2. Пользуясь таблицами истинности, докажите, что следующие формулы являются тождественно истинными:

1) 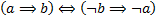— закон контрапозиции;

2) ;

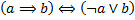3) .

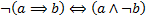Рекомендуемая литература:

Для лучшего ознакомления:

[1] YouTube: «Введение в логику» / Хекслет https://www.youtube.com/playlist?list=PLf1RW50cnBYeWgx6zue1rCJTVVuz9VnIP

Для полноценного изучения темы:

[2] Учебник: «Дискретная математика» / Новиков Фёдор Александрович / 2017

[3] YouTube: «Математическая логика и теория алгоритмов» / МФТИ, лектор — Дашков Евгений Владимирович

https://www.youtube.com/playlist?list=PL4_hYwCyhAvYls1eX-LmnQsmO3IANGRZv

[4] YouTube: «Введение в математическую логику и теорию алгоритмов» / Механико-математический факультет МГУ, лектор — Шехтман Валентин Борисович https://www.youtube.com/playlist?list=PLcsjsqLLSfNBbcIq4kESL7053mAvaUuFf

[5] YouTube: «Математическая логика и теория алгоритмов» / МФТИ, лектор — Мусатов Даниил Владимирович https://www.youtube.com/playlist?list=PL4_hYwCyhAvZjAmC7XFESNgWbG6wMteVm

[1] На ноль делить можно, но только само число ноль. Частное в этом случае не определено.

[2] Что означает знак 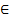— см. §2.

[3] Запись типа 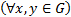, читаемая как «для любых икс и игрек из 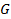», является сокращением для 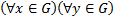, что читается аналогично как «для любого икс из 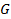и для любого игрек из ».

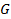[4] Формулы 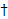и 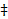являются аксиомами так называемого моноида (или, как ещё говорят, «полугруппы с единицей»). Формула 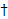выражает свойство «ассоциативности» операции .

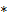[5] Мы докажем это свойство в следующих параграфах.

⇐ Предыдущая 12