
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Формальный язык
§1.1. Формальный язык
Для формализации математических текстов введём так называемые логические связки:
| Название | Прочтение | Обозначение |
| Отрицание | не | 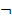
|
| Конъюнкция | и | 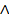
|
| Дизъюнкция | или | 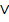
|
| Импликация | если …, то … | 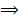
|
| Эквиваленция | тогда и только тогда, если и только если, в том и только том случае, согда | 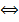
|
Вообще говоря, эти связки имеют больший смысл, чем просто сокращение слов разговорного языка. Интересующегося читателя мы обращаем к изучению математической логики и булевой алгебры — см. [1]–[5].
Все приведённые выше логические связки, за исключением одной, — «бинарные». Это означает, что они связывают два высказывания.
Пример 1.1.1. Запись 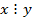 означает, что
означает, что  делится на
делится на  (к примеру,
(к примеру, 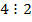 ). Тогда имеет место теорема, которую на формальном математическом языке можно выразить так:
). Тогда имеет место теорема, которую на формальном математическом языке можно выразить так: 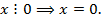 В переводе на русский: «если число делится на ноль, то это число само есть ноль»[1].
В переводе на русский: «если число делится на ноль, то это число само есть ноль»[1].
«Унарной» является связка 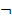 , она применяется к одному высказыванию.
, она применяется к одному высказыванию.
Пример 1.1.2. Запись 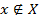 означает
означает  .
. 
Помимо логических связок нам также понадобятся так называемые кванторы:
| Название | Прочтение | Обозначение |
| Квантор всеобщности | для любого … | 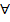
|
| Квантор существования | существует … | 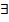
|
| Квантор существования и единственности | существует и единственен | 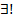
|
Слово квантор происходит от англ. quantity (количество); символ 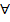 — от англ. any (любой); символ
— от англ. any (любой); символ 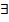 — от англ. exists (существует).
— от англ. exists (существует).
Используются разные синтаксические нормы, но мы будем окаймлять скобками кванторы вместе с переменными, которые они «связывают», а также следующие за ними высказывания.
Если  — некоторое свойство, то
— некоторое свойство, то 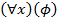 означает, что свойство
означает, что свойство  выполнено для всех объектов
выполнено для всех объектов 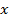 (обычно ещё указывают, откуда эти объекты берутся);
(обычно ещё указывают, откуда эти объекты берутся); 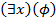 означает, что хотя бы для одного объекта
означает, что хотя бы для одного объекта 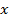 выполнено свойство
выполнено свойство  .
.
Пример 1.1.3. Запись

можно прочесть так: «для любых элементов 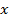 ,
, 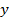 и
и 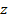 из множества
из множества 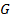 справедливо равенство
справедливо равенство 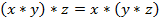 ». Кванторы могут также употребляться один за другим. Запись
». Кванторы могут также употребляться один за другим. Запись
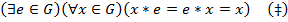
читается так: «во множестве  существует такой элемент
существует такой элемент 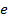 , что для любого элемента
, что для любого элемента 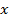 множества
множества 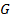 справедливо равенство
справедливо равенство 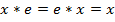 »[4].
»[4].
Очень важно понимать, что нельзя менять в порядке различные кванторы: 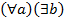 означает принципиально иное, нежели
означает принципиально иное, нежели 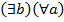 .
.
Польза записи математических текстов на формальном языке проявляется не только в компактности, но и в простоте международных коммуникаций. Замечу, опираясь на собственный опыт, что овладение таким формальным языком пригождается не только в математике, но и в других дисциплинах, когда нужно поспевать конспектировать лекции быстро читающих преподавателей.
Как и в примере 1.1.2 слово означает мы впредь будем заменять символом 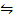 .
.
Символ 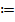 означает «равно по определению».
означает «равно по определению».
Пример 1.1.4. Число 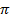 есть отношение длины окружности
есть отношение длины окружности 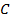 к её диаметру
к её диаметру 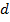 :
:
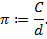
Установим некоторые соотношения, необходимые нам для дальнейшей работы. Их доказательство требует более детального обсуждения формальной теории, которая выходит далеко за рамки курса математического анализа, поэтому мы вынесли его в упражнения. Важно помнить, что это всё-таки — теорема 1.1.1:
| (1) Коммутативность конъюнкции | 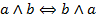
|
| (2) Коммутативность дизъюнкции | 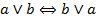
|
| (3) Ассоциативность конъюнкции | 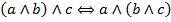
|
| (4) Ассоциативность дизъюнкции | 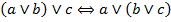
|
| (5) Дистрибутивность конъюнкции относительно дизъюнкции (слева и справа) | 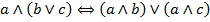 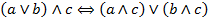
|
| (6) Дистрибутивность дизъюнкции относительно конъюнкции (слева и справа) | 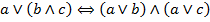 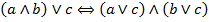
|
| (7) Идемпотентность конъюнкции | 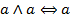
|
| (8) Идемпотентность дизъюнкции | 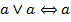
|
| (9) Снятие двойного отрицания | 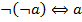
|
| (10) Законы де Моргана | 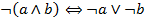 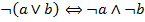
|
Заметим, что после установления коммутативности произвольной операции 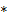 , из её дистрибутивности относительно другой операции
, из её дистрибутивности относительно другой операции 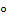 слева (или справа) следует её дистрибутивность относительно
слева (или справа) следует её дистрибутивность относительно 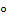 справа (соответственно, слева).
справа (соответственно, слева).
В курсе алгебры доказывается так называемое свойство обобщённой ассоциативности, согласно которому в выражении 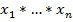 , если операция
, если операция 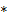 ассоциативна, расстановка скобок не играет роли, а потому все скобки можно опустить[5]. А если операция
ассоциативна, расстановка скобок не играет роли, а потому все скобки можно опустить[5]. А если операция 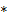 ещё и коммутативна, то не играет роли также порядок операндов. Примем это во внимание и для операций
ещё и коммутативна, то не играет роли также порядок операндов. Примем это во внимание и для операций 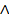 и
и 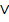 , коль скоро они и ассоциативны, и коммутативны. Таким образом, можно положить следующие определения:
, коль скоро они и ассоциативны, и коммутативны. Таким образом, можно положить следующие определения:
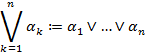
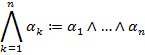
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|