I Актуализация. Пирамида. II Основная часть. Задание 8 № 901. Решение.

Стр 1 из 2Следующая ⇒

Тема: Пирамида и её свойства решения задач

Цель

Образовательная: Повторить свойства пирамиды; рассмотреть решения типовых задач ЕГЭ

Развивающая: развивать логическое и критическое мышление

Воспитательная: привить интерес к математике

Ход урока

I Актуализация

Пирамида

Пусть вне плоскости многоугольника задана точка P. Тогда фигура, образованная треугольниками , и многоугольником вместе с их внутренними областями называется пирамидой (n-угольной пирамидой).

Пирамида называется правильной, если ее основание — правильный многоугольник, а основание ее высоты — центр этого многоугольника.

Соотношения для правильной пирамиды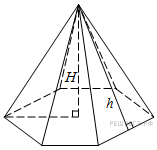

Пусть H — высота правильной пирамиды, h — ее апофема, — периметр основания пирамиды, — площадь основания, — площадь боковой поверхности, — площадь полной поверхности, V — объем правильной пирамиды. Тогда имеют место следующие соотношения:

II Основная часть

1. Задание 8 № 901

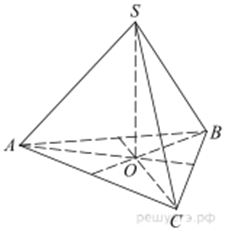
В правильной треугольной пирамиде SABC с вершиной S биссектрисы треугольника ABC пересекаются в точке O. Площадь треугольника ABC равна 2; объем пирамиды равен 6. Найдите длину отрезка OS.

Решение.

Отрезок 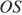высота треугольной пирамиды 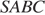, ее объем выражается формулой

Таким образом,

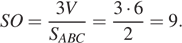
Ответ: 9.

12 Следующая ⇒