- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
IV этап. Итоги урока. Рефлексия
⇐ ПредыдущаяСтр 2 из 2
№ 1004.
Дано: а1х + b1y – c1 = 0
l1 : 3х – 1,5у + 1 = 0
а2х + b2y – c2 = 0
l2 : 2х – у – 3 = 0
Доказать: l1 úú l2.
Доказательство:
Условие l1 úú l2 выполнено, если а1 · b1 – а2 · b2 = 0, то есть
3 · (–1) – 2 · (–1,5) = 0
–3 + 3 = 0.
0 = 0 – верно, следовательно, l1 úú l2, что и требовалось доказать.
№ 1007.
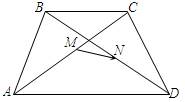
Рис. 3
Дано: АВСD – трапеция. M Î AC, AM = MC
N Î BD, BN = ND.
Доказать: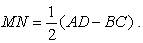 
Доказательство:
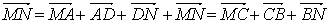(по правилу многоугольника).
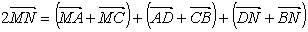, так как N и M – середины сторон BD и AC, то 
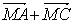= 0, 
= 0, 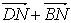следовательно, 2 
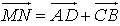или 2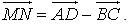 
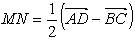, так как 
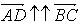и 
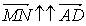, то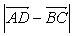 
= AD – BC, отсюда 
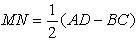, что и требовалось доказать
IV этап. Итоги урока. Рефлексия
Домашнее задание: подготовиться к контрольной работе; решить № 990, 1010 мне отчёт