
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Урок 19. Решение задач. I этап. Актуализация знаний учащихся. II этап. Самостоятельная работа. Вариант I (Баукова М). Вариант II (Харьковских М.). III этап. Решение задач
Урок 19. Решение задач
| Цель деятельности учителя | Создать условия для совершенствования навыков решения задач, подготовки к контрольной работе |
I этап. Актуализация знаний учащихся
1. Постарайтесь ответить на вопросы
– Сформулируйте теорему о разложении вектора по двум данным неколлинеарным векторам.
– Запишите формулы координат середины отрезка по координатам его концов.
– Напишите уравнение окружности с центром в точке В(4; 0), если она проходит через точку А(7; 4).
– Сформулируйте правило нахождения координат разности двух векторов.
– Напишите формулу для вычисления длины вектора по его координатам.
– Сформулируйте правило нахождения координат произведения вектора на число по заданным координатам вектора
II этап. Самостоятельная работа
Вариант I (Баукова М)
1. Окружность с центром в точке А(–5; 3) проходит через точку В(2; –1). Напишите уравнение этой окружности.
2. Напишите уравнение прямой, проходящей через начало координат и точку В(–2; 4).
3. Выясните взаимное расположение прямой х = –5 и окружности (х – 7)2 + (у – 6)2 = 81.
Вариант II (Харьковских М.)
1. Окружность с центром в точке М(2; –4) проходит через точку N(–3; 1). Напишите уравнение этой окружности.
2. Напишите уравнение прямой, проходящей через начало координат и точку С(–6; –3).
3. Выясните взаимное расположение прямой у = 25 и окружности (х – 5)2 + (у – 7)2 = 100. Мне фотоотчёт
III этап. Решение задач
1. Посмотрите и разберите решения задач № 997.
 Рис. 1
Рис. 1
Дано: А(3; 2); В(0; 5); С(–3; 2); D(0; –1).
Доказать: АВСD – квадрат.
Доказательство:
1) 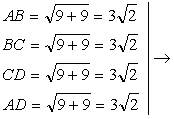 ромб (по признаку)
ромб (по признаку)
2) 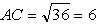
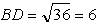 , следовательно, диагонали АС = ВD, следовательно, ромб АВСD – квадрат, что и требовалось доказать.
, следовательно, диагонали АС = ВD, следовательно, ромб АВСD – квадрат, что и требовалось доказать.
2. Решите в тетрадях № 999.
Дано: АВСD – параллелограмм. А (–4; 4); В(–5; –1); С(х; у); D(–1; 5).
Найти: (х; у).
Решение:
1) 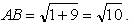
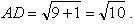
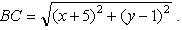

Так как в параллелограмме стороны попарно равны, то:

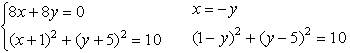
1 – 2у + у2 + у2 – 10у + 25 – 10 = 0 2у2 – 12у + 16 = 0 у1 = 4 у2 = 2
Если у = 4, то х = –4 – известна А(–4; 4). Если у = 2, то х = –2 – известна С(–2; 2).
3. Решить на доске и в тетрадях № 980.
 Рис. 2
Рис. 2
Дано: АВСD – ромб. АС Î Ох, BD Î Oy; AC = 4 см, BD = 10 см.
Написать уравнение АВ, ВС, СD, АD.
Решение:
1) А(–2; 0); С(2; 0); В(0; 5); D(0; –5).
2) А(–2; 0) и В(0; 5).

3) В(0; 5) и С(2; 0).
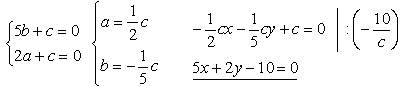
4) С(2; 0) и D(0; –5).

5) А(–2; 0) и D(0; –5).
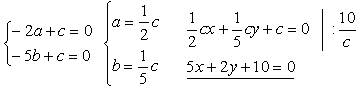
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|