Тема «Тригонометрические уравнения вида cos x = а»

Тема «Тригонометрические уравнения вида cos x = а»

Дорогие студенты! Сегодня вам необходимо еще раз повторить данную тему и решить уравнения вида cos x = а. Обратите внимание на этапы решения уравнений более сложного вида, а именно на последовательность преобразований.

Ваши выполненные задания жду 23 марта с 16.30 до 17.30.

Желаю удачи!

Справочный материал

Из определения косинуса следует, что -1 ≤ cos x ≤ 1 т.е. значение а 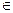[-1;1]. Если | а | > 1, то уравнение cos x = а не имеет корней.

Например: cos x = -1,8 и cos x = 3 не имеют корней.

Косинус угла – это абсцисса точки единичной окружности, полученной поворотом точки Р(1;0) вокруг начала координат.

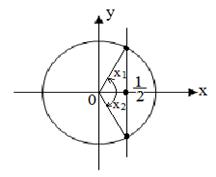Рассмотрим уравнение cos x =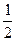

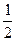Р₁

Р₂

Абсциссу

имеют две точки Р₁и Р_{2 .}

Значение 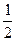имеет cos угла 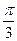(точка Р₁), а так же углы х = 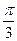+ 2pк, где к 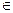Z.

Значение 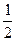имеет cos угла - 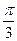(точка Р₂), а так же углы х =- 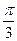+ 2pк, где к 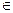Z.

Итак, все корни уравнения cos x = 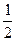можно найти по формуле:

х = ± 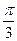+ 2pк, где к 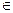Z.

На отрезке 0 £ х £ p уравнение имеет один корень х = 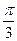. Число 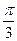называют арккосинусом числа 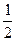и записывают arcсos =

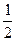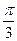
Вообще, уравнение cos x = а, где -1 £ а £ 1, имеет на отрезке 0 £ х £ p один корень. Этот корень называют арккосинусом числа а и обозначают arcсos а.

Определение: Арккосинусом числа а 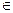[-1;1] называется такое число х 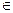[0;p], косинус которого равен а:

arcсos а = х, если cos х = а и 0 £ х £ p.

Вывод: Все корни уравнения cos x = а, где -1 £ а £ 1, х - любой угол, можно находить по формуле:

12 Следующая ⇒