Хелпикс

Главная

Контакты

Случайная статья



Методы решения уравнений, содержащих знак модуль.

⇐ ПредыдущаяСтр 4 из 4


Методы решения уравнений, содержащих знак модуль.


I) Уравнения вида  решаются следующим образом.

Если 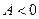, то корней нет.

Если 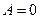, то уравнению  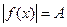соответствует уравнение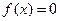

Если 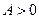, то уравнению  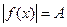соответствует равносильная совокупность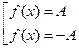

 

II) Уравнения вида  решаются следующим образом.

Способ №1

Уравнению 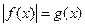 соответствует равносильная совокупность систем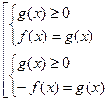

Способ №2

Уравнению 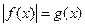 соответствует равносильная совокупность систем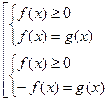

 

III) Уравнения вида  решаются следующим образом.

Способ №1

Уравнению 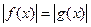 соответствует равносильное уравнение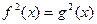

Способ №2

Уравнению 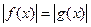 соответствует равносильная совокупность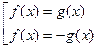

 

IV) Уравнения вида  и  решаются следующим образом.

Уравнению 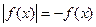 соответствует равносильное неравенство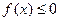

Уравнению 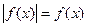 соответствует равносильное неравенство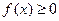

 

V) Общая схема решения уравнений содержащих знак модуль.

Например.

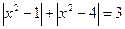
Найдем нули выражений, стоящих под знаком модуль.

 

 

 


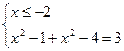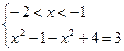I)               II)    III)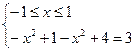

                                                          

 

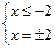
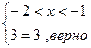
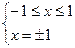
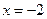
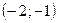                                                       - промежуток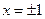              

I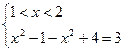V)            V)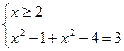  

 

                                     

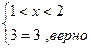
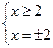
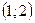 - промежуток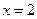                    

           

Ответ: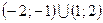

 

P. S. В уравнениях вида 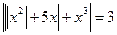 рекомендуется начинать раскрывать с внешнего модуля.


⇐ Предыдущая1234
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.