РЕШЕНИЯ ЗАДАЧ

РЕШЕНИЯ ЗАДАЧ

7 класс

1.Ответ. и 5.

Пусть х – ширина, тогда 1,5 х – длина прямоугольника. Из условий задачи получаем уравнение 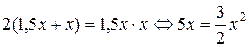. Отсюда, деля на х (¹ 0), получим 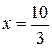; тогда

2. Ответ. 67.

Пусть a, b – цифры задуманного числа. Тогда из условий задачи 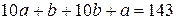, откуда a + b = 13. Учитывая, что a, b – цифры, отсюда получаем шесть возможных вариантов задуманного числа: 94, 85, 76, 67, 58, 49. Из этих вариантов только 67 – простое число.

3. Заметим, что все 9 карточек положить в ряд требуемым образом не получится. Это следует из того, что у каждой из карточек с числами 5 и 7 может быть только один сосед – карточка с числом 1. Значит, обе карточки 5 и 7 должны лежать с краев, а карточка с единицей должна соседствовать с каждой из них, что невозможно.

Выбрать 8 карточек и разложить их в ряд согласно требованиям задачи можно, например, так: 9, 3, 6, 2, 4, 8, 1, 5.

4. Треугольники ACG и BEF равны (G – точка пересечения AD и CE, F – точка пересечения BD и CE). Следовательно, ÐAGC = ÐBFE и AG = BF,

ÐCGD =ÐEFD. Значит, FD = GD. Окончательно получим: AG + GD = BF + FD или AD = BD.

5. Ответ. 6 уголков.

Пусть клетки квадрата 6x6 покрашены так, что больше ни одного уголка покрасить нельзя. Тогда в каждом квадратике 2x2 покрашено хотя бы 2 клетки, иначе в этом квадратике можно покрасить уголок. Разбивая квадрат 6x6 на 9 квадратиков2x2, получаем, что всего покрашено не меньше 18 клеток. Итак, покрашено не меньше 6 уголков.

На рисунке показано, как покрасить 6 уголков, чтобы больше ни одного уголка покрасить было нельзя.

⇐ Предыдущая 1 234 Следующая ⇒