Хелпикс

Главная

Контакты

Случайная статья



Запись правила нахождения производной сложной функции

⇐ ПредыдущаяСтр 2 из 2


4)                        

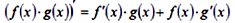
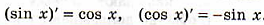
4)                                   5)          

2) Запись правила нахождения производной сложной функции

 Производная сложной функции равна произведению этой функции по промежуточной переменной g и на производную промежуточной переменной g по переменной x


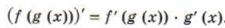
Решим пример 1 и найдем производную функции y’ = ((х2 +sin x)3)’

Какие же формулы нужны для решения задания?

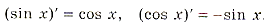(xn)’ = nxn-1;)         

 

 

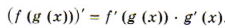
Алгоритм:

Пусть (х2 +sin x)3 = U;       U´ = (х2 +sin x) ´ =(2х +cos x);

 Тогда y’ = (U3)’ = 3 U2 U`=3(х2 +sin x)2(2х +cos x)

 

Можно заметить, что без знания формул и правил невозможно взять производную сложной функции, но для правильного расчета нужно видеть в дифференцировании основную функцию.

 

Задание 2: Найти производную функции: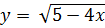

1. Определяем внешнюю и внутреннюю функции:

При упрощении получаем: (5-4х) = U,

т.е. ;

2. Находим производную по ходу чтения функции:

у’ = ’=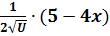

Задание 3: Найти производную функции: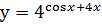

1. Определяем внешнюю и внутреннюю функции:

у = 4U – показательная функция

2. Находим производную по ходу чтения функции:

у’= ’=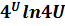

3 Домашнее задание.   Найти производную функции

1) ;

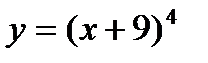2) ;

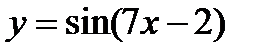3) ;

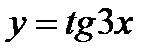4) ;

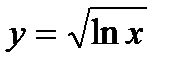ОЦЕНИВАЕТСЯ КОНСПЕКТ И ДОМАШНЕЕ ЗАДАНИЕ (ОТДЕЛЬНО)


⇐ Предыдущая12
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.