Хелпикс

Главная

Контакты

Случайная статья



Задача №2. Задача №3. Задача №4 ([1] №703). Найти объём конуса.. Решение.. Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒


Задача №2

Образующая конуса наклонена к плоскости основания под углом 30°, а высота конуса равна 12см. Найдите площадь боковой поверхности конуса и площадь полной поверхности.

Решение: 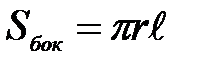, 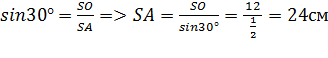Рассмотрим 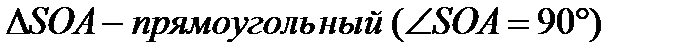По теореме Пифагора, имеем:  
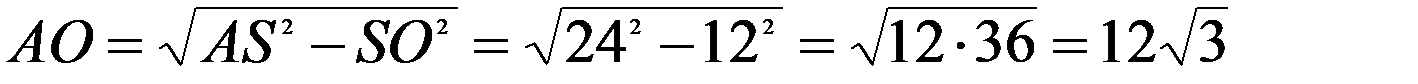
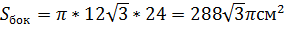
S
А
О

Площадь полной поверхности конуса называется сумма площадей боковой поверхности и основания.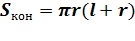          

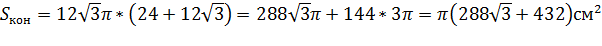
Ответ: .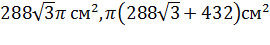

Задача №3

Образующая конуса равна 18 см и наклонена к плоскости основания под углом 60°.

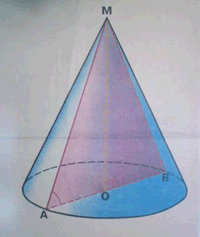Найдите радиус основания, высоту конуса, площадь осевого сечения и площадь полной поверхности конуса.

Дано:        конус.

AM=18 см,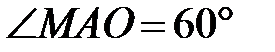

Найти AO, MO, площадь осевого сечения и площадь

полной поверхности конуса.

Решение:

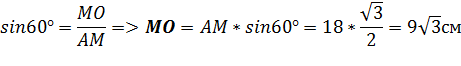
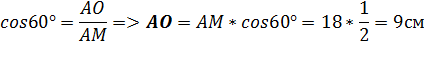
AB=2AO=18 см.

Площадь осевого сечения равна (площадь треугольника равна половине произведения основания на высоту, т.е.):

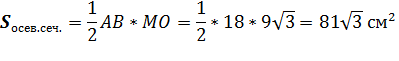
Площадь полной поверхности конуса равна

= =

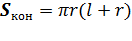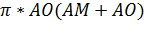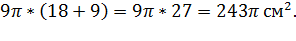
Ответ: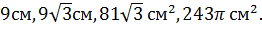


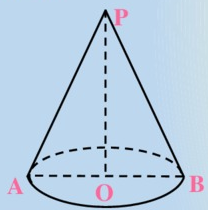
Задача №4 ([1] №703)

Найдите объём конуса, если площадь его основания равна Q,

а площадь боковой поверхности равна P.

Дано: конус,

Найти объём конуса.

Решение.

1)По теореме объем конуса равен одной трети произведения площади основания на высоту.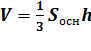

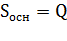по условию задачи,  необходимо найти.

2)

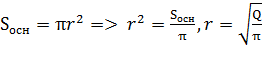
3) Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.

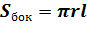,по условию задачи нам известна 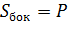,  найден в пункте 2)

Поэтому находим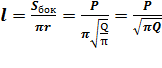 

4) 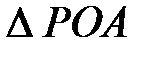-прямоугольный (∠POA = 90°), AP=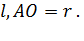

По теореме Пифагора имеем:

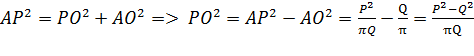, PO=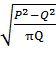

5)

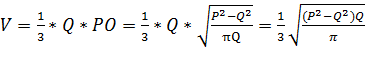
Ответ:  

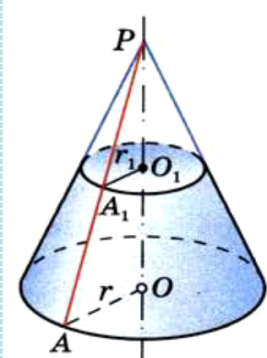2. Решение задач на вычисление элементов, площади поверхности и объёма усечённого конуса.


⇐ Предыдущая123Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.