Тема: Бесконечно убывающая геометрическая прогрессия. Решение задач.

Стр 1 из 2Следующая ⇒

Тема: Бесконечно убывающая геометрическая прогрессия. Решение задач.

Дата: 03.11.2020 г.

Группа: ПЦ-265

Цель урока: ознакомление учащихся с новым видом последовательности – бесконечно убывающей геометрической прогрессией.

Студенты должны знать: понятие бесконечной убывающей геометрической прогрессии.

Студенты должны уметь: применять на практике в заданиях понятия бесконечно убывающей геометрической прогрессии.

1.Актуализация опорных знаний

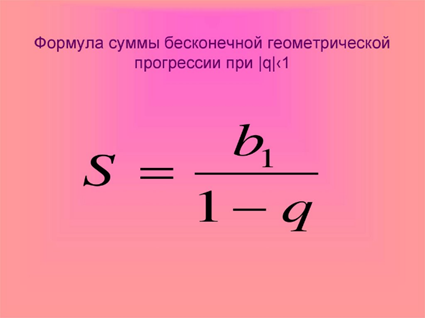
2. Решение упражнений.

Задание №1Вычислить первые пять членов геометрической прогрессии и написать формулу нахождения n-го члена, если b1 = 8 и q=0,5.

b1 = 8;

b2=b1⋅q = 8⋅0,5 = 4;

b3=b2⋅q = 4⋅0,5 = 2;

b4=b3⋅q = 2⋅0,5 = 1;

b5=b4⋅q = 1⋅0,5 = 0,5;

bn=b1⋅qn−1;

bn=8⋅0,5n−1.

Задание №2. Вычислить сумму первых пяти членов геометрической прогрессии, если b1 =8 и q=0,5.

I вариант решения

Рассмотрев первый пример, видим:

b1 =8, b2 = 4, b3 = 2, b4 = 1 и b5 = 0,5.

Сложив пять этих чисел, получим сумму (первых пяти членов последовательности):

Sn = S5 = b1 + b2 + b3 + b4 + b5 = 8+4+2+1+0,5 = 15,5.

II вариант решения

Используется 1-я формула:

Sn =bnq−b1q−1, где

n=5;

b1 = 8;

q=0,5;

bn = b5 =0,5 (т. к. n=5).

S5 = (0,5⋅0,5−8)(0,5−1) = 15,5.

III вариант решения

Используется 2-я формула:

Sn =b1(qn−1)q−1.

S5 = 8⋅(0,55−1)0,5−1 = 15,5.

Как видите, все три варианта решения приводят к одному и тому же результату.

Сумма первых пяти членов прогрессии равна S5 = 15,5.

Бесконечно убывающая геометрическая прогрессия — это прогрессия, у которой |q|<1

Для неё определяется понятие суммы членов бесконечно убывающей геометрической прогрессии как число, к которому неограниченно приближается сумма первых членов рассматриваемой прогрессии при неограниченном возрастании числа. S=b1/(1−q), q≠1

12 Следующая ⇒