III этап. Учебно-познавательная деятельность

⇐ ПредыдущаяСтр 2 из 2

III этап. Учебно-познавательная деятельность

Ввести понятие правильного многоугольника

1. прочитайте п. 109, 110.

2. Выполнить задания:

1) Какие правильные многоугольники уже рассматривались нами в курсе геометрии? (квадрат, равносторонний треугольник)

2) Приведите примеры такого выпуклого многоугольника, у которого:

а) все стороны равны, но он не является правильным (ромб с острым углом);

б) все углы равны, но он не является правильным (прямоугольник с неравными сторонами).

3. Посмотрите и запомните формулу для вычисления угла правильного многоугольника:

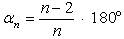
4. Решить задачи № 1081 (в) и 1083 (в) в тетрадях.

5. Сформулировать и доказать теорему об окружности, описанной около правильного многоугольника (с. 271,
рис. 307)

IV этап. Закрепление изученного материала

На простейших задачах отработать применение изученной формулы

1. Решить задачи № 1086 посмотрите решение, и 1084 (б, д) решите. 2. № 1080 и 1082 (устно)

№ 1086.

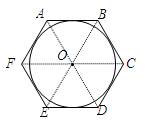Дано: ABCDEF – правильный 6-угольник. Доказать: биссектрисы углов пересекаются или совпадают. Доказательство: 1) Так как ÐA = ÐB = ÐC = ÐD = ÐE = ÐF (по определению), то

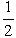ÐA =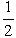

ÐB = …

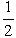ÐF = 60°. 2) Так как биссектрисы пересекаются в центре окружности, вписанной в 6-угольник, то ÐСОD = 60°, ÐCOE = 120°, ÐCOF = 180°, то есть биссектрисы или пересекаются или лежат на одной прямой (диаметр описанной окружности). Это справедливо для любого правильного многоугольника.

V этап. Итоги урока. Рефлексия

Домашнее задание:

изучить материалы пунктов 109–110; ответить на вопросы 1–3, с. 284; решить задачи № 1081 (д), 1083 (г), 1084 (а), 1129

⇐ Предыдущая 12