
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Дополнительные задачи. ОТВЕТЫ. Невырожденные системы линейных уравнений. Неопределенные системы линейных уравнений. Фундаментальная система решений. Дополнительные задачи
4. Дополнительные задачи
4.1.Матричным методом решите систему уравнений:
а) 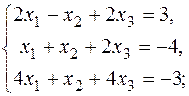 б)
б) 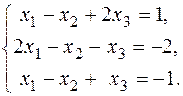
4.2.Решите по правилу Крамера систему уравнений:
а) 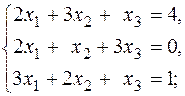 б)
б) 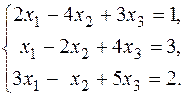
4.3. Методом Гаусса решите систему уравнений:
а) 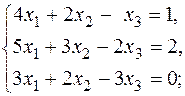 б)
б)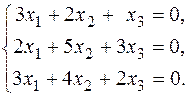
4.4.Найдите общее решение системы линейных уравнений через свободные неизвестные:
а)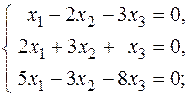 б)
б) 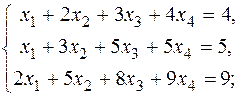
в) 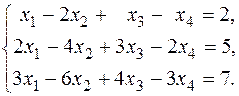
4.5.Найдите общее решение системы линейных уравнений через нормальную фундаментальную систему решений:
а)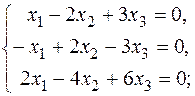 б)
б)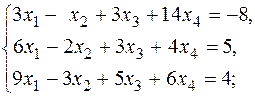
в) 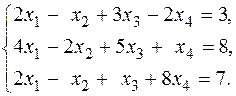
ОТВЕТЫ
1. Невырожденные системы линейных уравнений
1.1. а) x1 = 2, x2 = –5, x3 = 3, 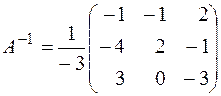 ; б)x1 = –1, x2 = 3,
; б)x1 = –1, x2 = 3,
x3 = 2, 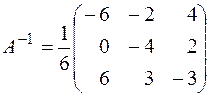 .1.2. а) x1 = –2, x2 = 0, x3 = 1,
.1.2. а) x1 = –2, x2 = 0, x3 = 1, 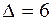 ; б) x1 = 1, x2 = –1, x3 = 2,
; б) x1 = 1, x2 = –1, x3 = 2, 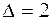 . 1.3.а) x1 = 2, x2 = –1, x3 = 3; б) x1 = 1, x2 = 0, x3 = –1, x4 = 2. 1.4.а) x1 = 1, x2 = –1, x3 = 2,
. 1.3.а) x1 = 2, x2 = –1, x3 = 3; б) x1 = 1, x2 = 0, x3 = –1, x4 = 2. 1.4.а) x1 = 1, x2 = –1, x3 = 2, 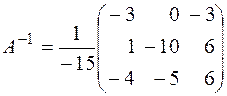 ; б) x1 = –2, x2 = 1, x3 = –2,
; б) x1 = –2, x2 = 1, x3 = –2, 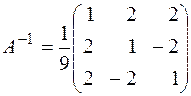 . 1.5.а) x1 = 2, x2 = –1, x3 = –3,
. 1.5.а) x1 = 2, x2 = –1, x3 = –3, 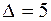 ;
;
б) x1 = 1, x2 = 2, x3 = –2, 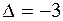 . 1.6.а) x1 = –3, x2 = 2, x3 = 1; б) x1 = 2, x2 = –1,
. 1.6.а) x1 = –3, x2 = 2, x3 = 1; б) x1 = 2, x2 = –1,
x3 = 0, x4 = 1.
2. Неопределенные системы линейных уравнений
2.1.а) x1 = 2t–3, x2 = 6t–7, x3 = 5t–7, x4 = t, 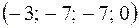 ; б) x1 = –7t1–9,
; б) x1 = –7t1–9,
x2 = 5+5t1+t2, x3 = t1, x4 = t2, 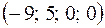 . 2.2. а)x1 = 4t, x2 = t, x3 = –5t;
. 2.2. а)x1 = 4t, x2 = t, x3 = –5t;
б) x1 = t1, x2 = 2t1–8t2, x3 = –3t2, x4 = t2. 2.3 а) x1 = 19–7t, x2 = t, x3 = 14–5t,
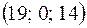 ; б) x1 = 2+t1–t2, x2 = 3–2t1+t2, x3 = t1, x4 = t2,
; б) x1 = 2+t1–t2, x2 = 3–2t1+t2, x3 = t1, x4 = t2, 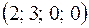 .
.
2.4.а)x1 = 14t, x2 = 21t, x3 = t, x4 = t; б) x1 = –t1+t2, x2 = –t1–3t2, x3 = t1, x4 = t2.
3. Фундаментальная система решений
3.1. а)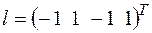 ; б)
; б)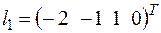 ,
, 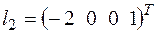 .
.
3.2.а)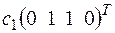 +
+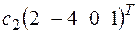 ; б)
; б) 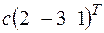 . 3.3.а)
. 3.3.а)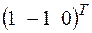 +
+
+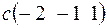 ; б)
; б) 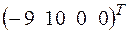 +
+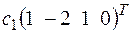 +
+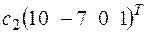 .
.
3.4.а)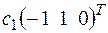 +
+ 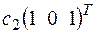 ; б)
; б) 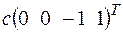 . 3.5.а)
. 3.5.а)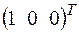 +
+
+ 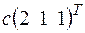 ; б)
; б)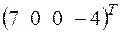 +
+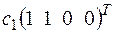 +
+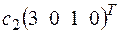 .
.
4. Дополнительные задачи
4.1. а) x1 = 1, x2 = –3, x3 = –1, 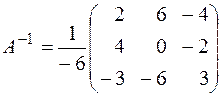 ; б)x1 = 3, x2 = 6,
; б)x1 = 3, x2 = 6,
x3 = 2, 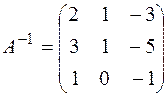 . 4.2. а) x1 = –1, x2 = 2, x3 = 0,
. 4.2. а) x1 = –1, x2 = 2, x3 = 0, 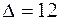 ; б) x1 = –1,
; б) x1 = –1,
x2 = 0, x3 = 1, 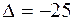 . 4.3.а) x1 = –1, x2 = 3, x3 = 1; б) x1 = 0, x2 = 0, x3 = 0.
. 4.3.а) x1 = –1, x2 = 3, x3 = 1; б) x1 = 0, x2 = 0, x3 = 0.
4.4. а) x1 = t, x2 = –t, x3 = t; б) x1 = 2+t1–2t2, x2 = 1–2t1–t2, x3 = t1, x4 = t2;
в) x1 = 1+2t1+t2, x2 = t1, x3 = 1, x4 = t2. 4.5. а)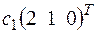 +
+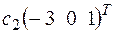 ;
;
б)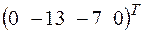 +
+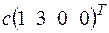 ; в)
; в)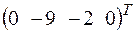 +
+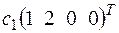 +
+
+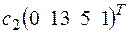 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|