
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Бросаются одновременно два игральных кубика. Какова вероятность того, что сумма очков будет равна 12?
3. Бросаются одновременно два игральных кубика. Какова вероятность того, что сумма очков будет равна 12?
Решение: Классическое определение вероятности события: Р(А) = 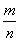 , где m - общее число элементарных событий, n - число элементарных событий, благоприятствующих событию А.
, где m - общее число элементарных событий, n - число элементарных событий, благоприятствующих событию А.
Чтобы сумма выпавших очков была равна 12, должны произойти одновременно два события: В - на первом кубике выпадет <6>, С - на втором кубике выпадет тоже <6>. Причем, события В и С независимые. Тогда Р(В) = 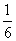 и Р(С) =
и Р(С) = 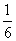 , т.к. m = 6 (может выпасть грань с цифрами: 1, 2, 3, 4, 5, 6), n= 1 (т.к. цифра 6 может вапасть только один раз).
, т.к. m = 6 (может выпасть грань с цифрами: 1, 2, 3, 4, 5, 6), n= 1 (т.к. цифра 6 может вапасть только один раз).
Рассмотрим событие А, состоящее в том, что одновременно произошли и событие В, и событие С, т.е. А = В С. Учитывая, что события В и С независимые, получаем
Р(А) = P(B C) = P(B) Р(С) = 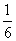
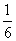 =
= 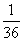 .
.
Возможно решение с помощью таблицы:
| 1 | ||||||
| А |
Буква А проставлена в тех клетках, где сумма номеров строки и столбца равна 12. Таких клеток получилось 1, а всего клеток 6*6=36, значит, Р(А) = m/n = 1/36.
4. В ящике лежат 6 красных и 6 синих шаров. Наудачу вынимают 8 шаров. Определите вероятность события А - все выбранные шары красные.
Решение: Р(А) = 0, т.к. это событие А - невозможное.
5. Два телевизионщика делают сюжет на одну и ту же тему. Вероятность того, что сюжет 1-го телевизионщика попадет в эфир (событие А) составляет 0,4, а 2-го (событие В) - 0,7. Оба журналиста работают одновременно для одной и той же передачи. Какова вероятность того, что в эфир пройдет сюжет хотя бы одного из них (событие С)?
Решение: Событие С=А+В, тогда Р(С)=Р(А+В). Учитывая, что события А и В совместимые (т.к. в эфире могут показать только один сюжет на одну и ту же тему) и независимые, то Р(С)=Р(А+В)=Р(А)+Р(В)-Р(АВ).
Продолжая рассуждать, замечаем, что события А и В независимые, значит
Р(С) = Р(А+В) = Р(А)+Р(В)-Р(АВ) = Р(А)+Р(В)-Р(А)Р(В) = 0,4+0,7-0,4*0,7=0,82.
6. В папку положили 7 аналитических статей и 4 очерка. Редактор вынимает один материал и, не возвращая его обратно в папку, вынимает второй. Какова вероятность того, что оба вынутых материала окажутся очерком?
Решение: Классическое определение вероятности события: Р(А) = 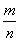 , где m - общее число элементарных событий, n - число элементарных событий, благоприятствующих событию А.
, где m - общее число элементарных событий, n - число элементарных событий, благоприятствующих событию А.
Пусть В - событие, состоящее в том, что очерк достали в первый раз. Учитывая, что Р(В) = 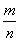 и что в нашем случае m = 7+4 =11, n = 4, получаем Р(В) =
и что в нашем случае m = 7+4 =11, n = 4, получаем Р(В) = 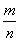 =
= 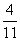 .
.
Пусть С - событие, состоящее в том, что очерк достали во второй раз (при условии, что и в первый раз достали очерк). Вычислим вероятность события С. РВ(С) = 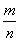 , где m = 11 - 1 = 10, т.к. один материал достали раньше, n = 4 - 1 = 3, т.к. один очерк достали в первый раз. Таким образом, РВ(С) =
, где m = 11 - 1 = 10, т.к. один материал достали раньше, n = 4 - 1 = 3, т.к. один очерк достали в первый раз. Таким образом, РВ(С) = 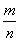 =
= 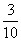 .
.
Пусть D - событие, состоящее в том, что очерк достали оба раза. Тогда D = B * C.
Учитывая, что события B и C зависимые, получаем:
Р(D) = P(B * C) = P(B) * РВ(С) = 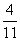 *
* 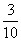 =
= 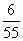 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|