Найти абсциссы точек, в которых касательные к графику функции параллельны оси абсцисс.

4. Найти абсциссы точек, в которых касательные к графику функции параллельны оси абсцисс.

Если касательная параллельна оси абсцисс, следовательно угол между касательной и положительным направлением оси 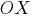равен нулю, следовательно тангенс угла наклона касательной равен нулю. Значит, значение производной функции 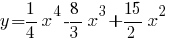в точках касания равно нулю.

а) Найдем производную функции .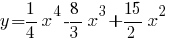

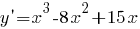
б) Приравняем производную к нулю и найдем значения 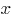, в которых касательная параллельна оси :

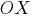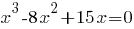
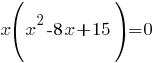
Приравняем каждый множитель к нулю, получим:

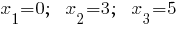
Ответ: 0;3;5

5. Написать уравнения касательных к графику функции 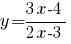, параллельных прямой .

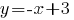Касательная параллельна прямой 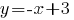. Коэффициент наклона этой прямой равен -1. Так как касательная параллельна этой прямой, следовательно, коэффициент наклона касательной тоже равен -1. То есть мы знаем коэффициент наклона касательной, а, тем самым, значение производной в точке касания.

Это второй тип задач на нахождение уравнения касательной.

Итак, у нас дана функция 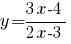и значение производной в точке касания.

а) Найдем точки, в которых производная функции 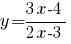равна -1.

Сначала найдем уравнение производной.

Нам нужно найти производную дроби.

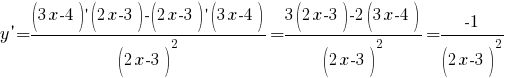
Приравняем производную к числу -1.

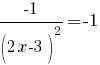
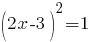
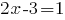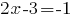
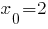или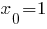

б) Найдем уравнение касательной к графику функции 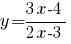в точке .

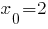Найдем значение функции в точке .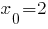

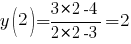
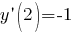(по условию)

Подставим эти значения в уравнение касательной:

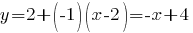б) Найдем уравнение касательной к графику функции 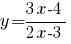в точке .

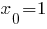Найдем значение функции в точке .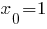

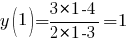
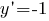(по условию).

Подставим эти значения в уравнение касательной:

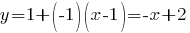Ответ: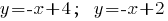

7. Задача Составьте уравнение касательной к графику функции y = x³ – 4x + 1в точке M(3; – 2).

Решение. Точка M(3; – 2) является точкой касания, так как

f(3) =

1. x₀ = 3 – абсцисса точки касания.
2. f(3) = – 2.
3. f '(x) = x² – 4, f '(3) = 5.
y = – 2 + 5(x – 3), y = 5x – 17 – уравнение касательной.

8 Задача Напишите уравнения всех касательных к графику функции y = – x² – 4x + 2, проходящих через точку M(– 3; 6).

Решение. Точка M(– 3; 6) не является точкой касания, так как f(– 3) ≠ 6 (рис. 2).

1. x₀ – абсцисса точки касания.
2. f(x₀) = – a² – 4a + 2.
3. f '(x) = – 2x – 4, f '(a) = – 2a – 4.
4. y = – a² – 4a + 2 – 2(a + 2)(x – a) – уравнение касательной.

Касательная проходит через точку

M (-3;6), следовательно, ее координаты удовлетворяют уравнению касательной.

6 = – x₀² – 4x₀ + 2 – 2(x₀ + 2)(– 3 – x₀),
x₀² + 6x₀ + 8 = 0 .

x₀= – 4, x₀ = – 2.

Если x₀ = – 4, то уравнение касательной имеет вид y = 4x + 18.

Если x₀ = – 2, то уравнение касательной имеет вид y = 6.

Во втором типе ключевыми задачами будут следующие:

· касательная параллельна некоторой прямой (задача 3);

· касательная проходит под некоторым углом к данной прямой (задача 4).

9. Задача Напишите уравнения всех касательных к графику функции y = x³ – 3x² + 3, параллельных прямой y = 9x + 1.

Решение.

1. x₀ – абсцисса точки касания.

2. f(x₀) = x₀³ – 3x₀² + 3.

3. f '(x) = 3x² – 6x, f '(x₀) = 3x₀² – 6x₀.

Но, с другой стороны, f '(x₀) = 9 (условие параллельности). Значит, надо решить уравнение 3x₀² – 6x₀ = 9. Его корни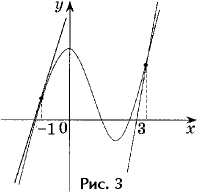

x₀ = – 1, x₀ = 3 (рис. 3).

4. 1) x₀ = – 1;
2) f(– 1) = – 1;
3) f '(– 1) = 9;
4) y = – 1 + 9(x + 1);

y = 9x + 8 – уравнение касательной;

1) x₀ = 3;
2) f(3) = 3;
3) f '(3) = 9;
4) y = 3 + 9(x – 3);

y = 9x – 24 – уравнение касательной.

Задача 4. Напишите уравнение касательной к графику функции y = 0,5x² – 3x + 1, проходящей под углом 45° к прямой y = 0 (рис. 4).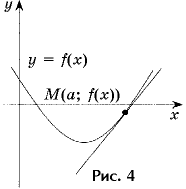

Решение. Из условия f '(a) = tg 45° найдем a: a – 3 = 1 ^ a = 4.

1. x₀= 4 – абсцисса точки касания.
2. f(4) = 8 – 12 + 1 = – 3.
3. f '(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4).

y = x – 7 – уравнение касательной.

Несложно показать, что решение любой другой задачи сводится к решению одной или нескольких ключевых задач.

Рассмотрим в качестве примера следующую задачу.

Напишите уравнения касательных к параболе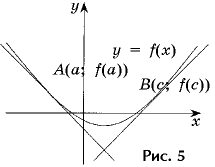

y = 2x² – 5x – 2, если касательные пересекаются под прямым углом и одна из них касается параболы в точке с абсциссой 3 (рис. 5).

Решение. Поскольку дана абсцисса точки касания, то первая часть решения сводится к ключевой задаче 1.

1. x₀= 3 – абсцисса точки касания одной из сторон прямого угла.
2. f(3) = 1.
3. f '(x) = 4x – 5, f '(3) = 7.
4. y = 1 + 7(x – 3), y = 7x – 20 – уравнение первой касательной.

2.Пусть a – угол наклона первой касательной. Так как касательные перпендикулярны, то – угол наклона второй касательной. Из уравнения y = 7x – 20 первой касательной имеем tg a = 7.

Найдем tg() = - ctg = -

Это значит, что угловой коэффициент второй касательной равен - .

Дальнейшее решение сводится к ключевой задаче 3.

Пусть B(c; f(c)) есть точка касания второй прямой, тогда

f´(c) = 4c – 5c = - => c =

c = – абсцисса второй точки касания.
2. f ( = -
3. f ´ ( = -
4. y = -

y = – уравнение второй касательной.

Примечание. Угловой коэффициент касательной может быть найден проще, если учащимся известно соотношение коэффициентов перпендикулярных прямых k₁•k₂ = – 1.

⇐ Предыдущая 12