
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Просмотрите видеоурок, изучите конспект, запишите в справочник алгоритм нахождения касательной. Разберите примеры решения задач. Оформите работу в тетради.
Просмотрите видеоурок, изучите конспект, запишите в справочник алгоритм нахождения касательной. Разберите примеры решения задач. Оформите работу в тетради.
Уравнение касательной к графику функции
Пусть дана функция f, которая в некоторой точке x0 имеет конечную производную f (x0). Тогда прямая, проходящая через точку (x0; f (x0)), имеющая угловой коэффициент f ’(x0), называется касательной.
А что будет, если производная в точке x0 не существует? Возможны два варианта:
1. Касательная к графику тоже не существует. Классический пример — функция y = |x| в точке (0; 0).
2. Касательная становится вертикальной. Это верно, к примеру, для функции y = arcsin x в точке (1; π/2).
Уравнение касательной
Всякая невертикальная прямая задается уравнением вида y = kx + b, где k — угловой коэффициент. Касательная — не исключение, и чтобы составить ее уравнение в некоторой точке x0, достаточно знать значение функции и производной в этой точке.
Итак, пусть дана функция y = f (x), которая имеет производную y = f ’(x) на отрезке [a; b]. Тогда в любой точке x0 ∈ (a; b) к графику этой функции можно провести касательную, которая задается уравнением:
y = f ’(x0) · (x − x0) + f (x0)
Здесь f ’(x0) — значение производной в точке x0, а f (x0) — значение самой функции.

1. Задача. Дана функция y = x3. Составить уравнение касательной к графику этой функции в точке x0 = 2.
Уравнение касательной: y = f ’(x0) · (x − x0) + f(x0). Точка x0 = 2 нам дана, а вот значения f (x0) и f ’(x0) придется вычислять.
Для начала найдем значение функции. Тут все легко: f (x0) = f (2) = 23 = 8;
Теперь найдем производную: f ’(x) = (x3)’ = 3x2;
Подставляем в производную x0 = 2: f ’(x0) = f ’(2) = 3 · 22 = 12;
Итого получаем: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16.
Это и есть уравнение касательной.
2. Задача. Составить уравнение касательной к графику функции f (x) = 2sin x + 5 в точке x0 = π/2.
В этот раз не будем подробно расписывать каждое действие — укажем лишь ключевые шаги. Имеем:
f (x0) = f (π/2) = 2sin (π/2) + 5 = 2 + 5 = 7;
f ’(x) = (2sin x + 5)’ = 2cos x;
f ’(x0) = f ’(π/2) = 2cos (π/2) = 0;
Уравнение касательной:
y = 0 · (x − π/2) + 7 ⇒ y = 7
В последнем случае прямая оказалась горизонтальной, т.к. ее угловой коэффициент k = 0. Ничего страшного в этом нет — просто мы наткнулись на точку экстремума.
3. Написать уравнение касательной к графику функции 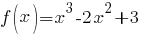 в точке
в точке 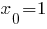 .
.
а) Найдем значение функции в точке 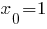 .
.
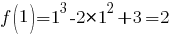 .
.
б) Найдем значение производной в точке 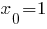 . Сначала найдем производную функции
. Сначала найдем производную функции 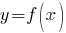
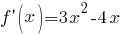
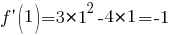
Подставим найденные значения в уравнение касательной:
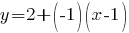
Раскроем скобки в правой части уравнения. Получим: 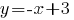
Ответ: 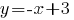 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|