ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 12. ИССЛЕДОВАНИЕ ФУНКЦИЙ. ВЫПУКЛОСТЬ, ВОГНУТОСТЬ, ТОЧКИ ПЕРЕГИБА. Асимптоты

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 12

ИССЛЕДОВАНИЕ ФУНКЦИЙ

ВЫПУКЛОСТЬ, ВОГНУТОСТЬ, ТОЧКИ ПЕРЕГИБА

График функции y=f(x) будет выпуклым на интервале 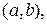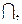если во всех точках этого интервала график функции располагается ниже любой ее касательной. В этом случае

f’’(x)<0. Если f’’(x)>0, то график будет вогнутым, .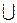

Точка, в которой отделяется выпуклая часть от вогнутой , будет точкой перегиба. Точки, в которых f’’(x)=0 или не существуют, называются критическими точками 2-го рода.

Найти интервалы выпуклости и точки перегиба функций.

1. Пусть 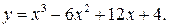Найдем первую и вторую производные:

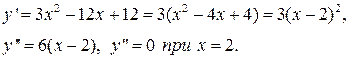
Получим такие интервалы

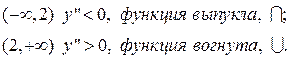
При x=2 y=12 и точкой перегиба будет (2, 12).

2. Возьмем 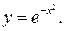Здесь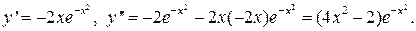

Вторая производная равна нулю, когда

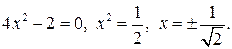
При таких х у= 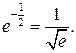Точками перегиба будут

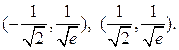
Графиком функции является куполообразная кривая.

Асимптоты

Если 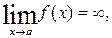то прямая х=а является вертикальной асимптотой кривой. Правая наклонная асимптота y=kx+b существует, если существуют пределы

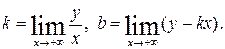
Если существуют пределы при 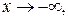то будем иметь и левую наклонную асимптоту.

1. Найти асимптоты кривой

Приравнивая знаменатель нулю 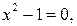получим две вертикальные асимптоты х=-1 и х=1.

Ищем параметры для наклонной асимптоты y=kx+b. У нас

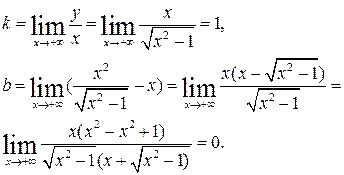
Следовательно, у=х – правая наклонная асимптота.

При 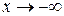получим 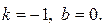Левой асимптотой будет у=-х. При построении графика этой кривой нужно учесть, что эта функция четная и поскольку о.д.з. здесь 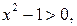то при 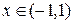функция не существует.

12 Следующая ⇒